本文是学习Neural ODE过程中的第一篇个人笔记
为了较为全面地理解其中的VAE思想,首先需要学习一些基础知识,例如Variational Inference变分推断
比较复杂的其他过程,包括ODE、伴随方法、以及更进阶的SDE,会在之后的笔记中再记录。
前言 Introduction
最近,估计是搜了若干比较数学理论的东西,被B站的推荐系统疯狂轰炸,各种统计学、数据科学、机器学习的视频都在强调“变分推断”。然而,我总是看不懂,反复问自己“为什么要使用变分推断?”,“为什么大家都在强调变分推断很重要,最新的研究也一直层出不穷?”。
起初,我觉得这就是一个高大上的名词,反正在CV、NLP乃至语音,大力出奇迹的事情多了去了,用得着再回到统计理论这边吗?感觉统计理论距离落地应用总是很远,用的数据集有很多也是比较玩具的(理想化)。然而万万没想到,项目确实碰到了这个问题,需要用到类似Neural ODE的方法,基于观测来建模一个过程的内部状态变化,那么深入了解变分推断就是很重要的工作了。
虽然,我确实接触过VAE(变分自编码器Variational Auto-Encoder)的概念,知道自编码器确实可以通过高斯分布的$\mu$和$\sigma$的显式形式,来代替隐式的表征$z$,来实现更加可控地重构图像$x$,也知道为了保证这一点,需要找出一个ELBO(证据下界,Evidence Lower Bound)作为网络的优化目标。但是从头到尾,“变分”这个名词总如天外来客,没有由来。
PS:下面的各种过程主要都是变量代换,以及一些现成的公式,不涉及很深的数学理论,可以根据每章首尾的前后衔接,按需跳读。
贝叶斯公式 Bayes Formula
事实上,这仍然是最底层的贝叶斯理论引出,这里就参考B站视频[1]。首先讲一个CV的例子:有观测到的图像$x$,其隐式状态是one-hot的类别编码$z$。例如,有三个类A、B、C,如果这个图像是A类,则$z=(1, 0, 0)^\top$。为了知道这个图像到是否真的属于类别A,需要知道相应的概率。也就是给定观测值$x$,其隐式状态应该属于$z$的概率。这显然是一个条件概率,写作$p(z|x)$。根据贝叶斯公式,有:
$$
p(z|x)=\frac{p(x|z)p(z)}{p(x)}
$$
各个项表达的意思是:1)分子:$p(x|z)p(z)=p(x,z)$,观测值$x$和隐式状态$z$的联合概率(Joint Probability),就是观测值$x$和隐式状态$z$同时出现的概率,其中$p(z)$为隐式状态出现的先验概率(Prior Probability),$p(x|z)$就是隐式状态固定的条件下,样本出现的概率;2)分母:$p(x)=\int_0^\mathrm{\infty} p(x,z) dz$,观测值本身出现的先验概率,就是所有可能的隐式状态$z$下,观测值$x$出现的概率之和;3)总体:$p(z|x)$后验概率(Posterior Probability),在观测值已经出现的这一种先验下(分母),观测值与隐式状态同时出现的概率(分子)。
很多人都知道在学贝叶斯的过程中,他们会被告知$p(z|x) \sim p(x|z)p(z)$,因为一旦$x$确定下来了,$p(x)$就是个常数。但是,这个常数到底能不能省略呢?如果要知道$p(z|x)$的确切数值的话,其实是必须知道的。按照我个人的理解,如果观测值$x$是一个过于罕见或者常见的样本,导致$p(x)$本身非常小或者非常大,那么这将会决定$p(z|x)$的最终数值,联合概率$p(x,z)$再大再小也不能与后验概率$p(z|x)$划等号。
换而言之,不同的观测值$x$决定了不同的$p(x)$,而不同的$p(x)$最终决定了$p(z|x)$的取值。例如,这个B站视频[1]里面的一个可视化例子,横轴为不同的隐式状态取值$z$,纵轴为不同方法计算出的概率取值,取不同的观测值$x$:
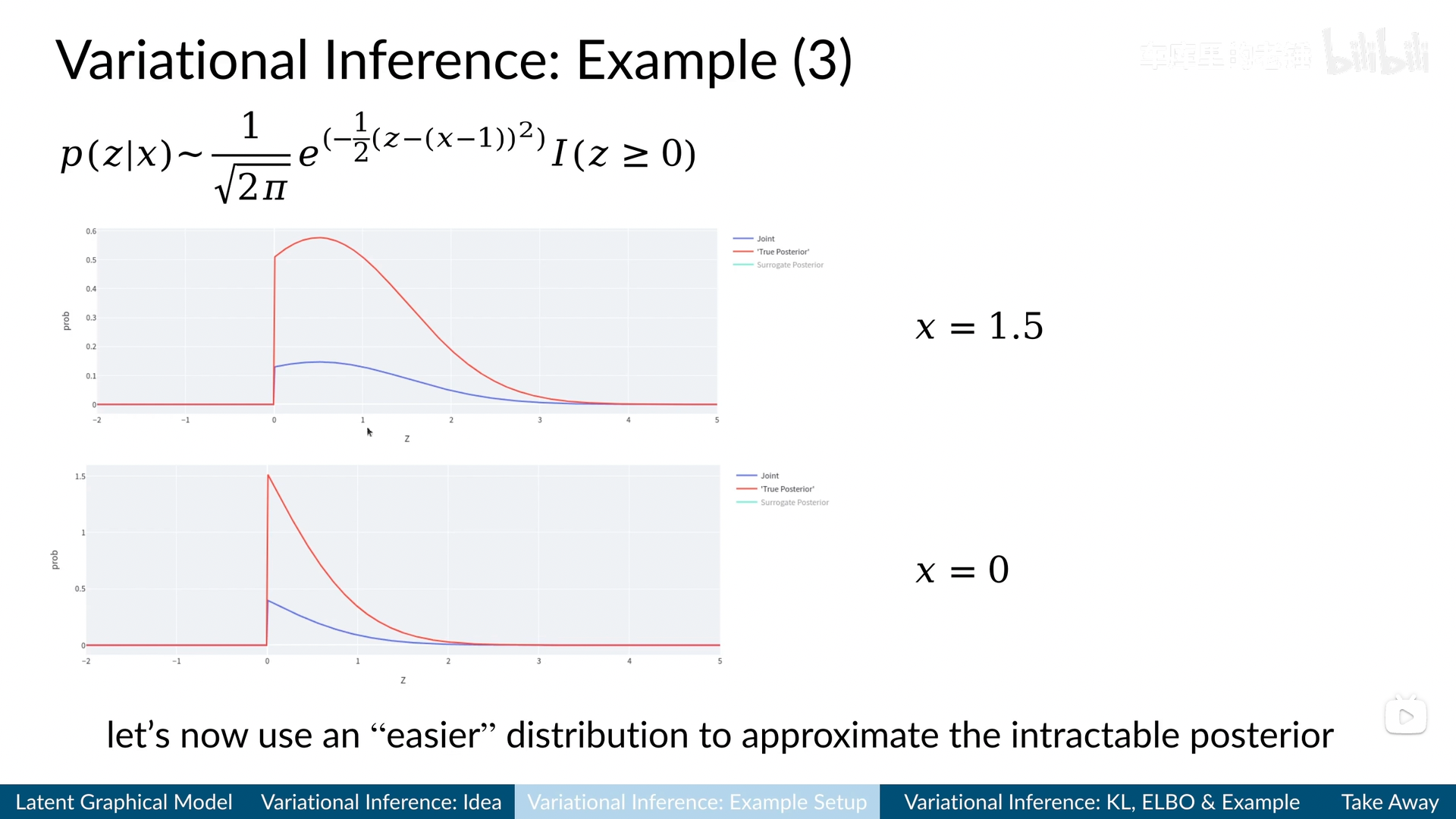
与真正带有先验$p(x)$的后验概率(红线“True Posterior”,通过数值计算得到)有非常明显的不同。
视频截图来自B站[1]
所以,正如上面的截图中所说,需要找到一个更简单的分布,来逼近这个因为先验概率$p(x)=\int_0^\mathrm{N} p(x,z) dz$比较难算(因为没办法穷尽所有的可能,去找到观测值$x$本身出现的概率),而导致本身比较难算的后验概率$p(z|x)$。
变分推断 Variational Inference
为了解决这个问题,变分的思想就是使用一些可以参数化的(例如高斯分布可以用$\mu$和$\sigma$两个参数来表示)、更简单的概率分布,来近似一个难算的概率分布,例如在这边就是后验分布$p(z|x)$。从泛函的角度来讲,就是由一族函数构成的空间(类比机器学习里面常提的参数空间),我们要通过变化输入参数(Variable),来找到这个空间中最能满足近似目标的一个函数。
至于为什么叫推断,实际上还是前面的一套贝叶斯的思路,用先验分布和联合分布来推断后验分布,所以如果不用变分操作,就可以直接叫贝叶斯推断(Bayesian Inference)了。
首先,为了逼近、近似一个分布,肯定需要衡量我们预测的分布和目标分布的相似度。最常用的就是KL散度(Kullback-Leibler Divergence):
$$
\begin{align}
D(q||p) = & \ H(q, p)-H(q) \nonumber \\
= & \ \int q(x)\log\frac{q(x)}{p(x)}dx \nonumber \\
= & \ \mathbb{E}_{x\sim q}[\log q(x) - \log p(x)] \nonumber \\
\end{align}
$$
由于后验分布$p(z|x)$中,难算的主要是$p(x)$,所以我们不能直接近似它,而且在近似过程中肯定不能再引入$x$了,那么只剩下隐式状态$z$。我们用来近似$p(z|x)$的后验概率就记作$q_\theta(z)$,其中$\theta$就是参数。那么,基于KL散度来衡量两者的相似度,有这样的计算过程:
$$
\begin{align}
& D(q_{\theta}(z)||p(z|x)) \nonumber \\
& = \ \mathbb{E}_{z\sim q} [ \log q_{\theta}(z) - \log \frac{p(x, z)}{p(x)} ] \nonumber \\
& = \ \mathbb{E}_{z\sim q} [ \log q_{\theta}(z) - \log p(x, z) ] + \log p(x)
\end{align}
$$
其中,$\log p(x)$和$z$没关系,所以用期望公式的$q_\theta(z)$来加权求和之后,还是自己本身,所以可以从里面拿出来。那么,我们整理上述公式,$\log p(x)$等于式子(1)中的期望项的负号和KL散度的组合:
$$
\begin{align}
\log p(x) = & \ \mathbb{E}_{z\sim q} [ \log p(x, z) - \log q_{\theta}(z) ] \nonumber \\
& + D(q_{\theta}(z)||p(z|x)) \nonumber \\
\geq & \ \mathbb{E}_{z\sim q} [ \log p(x, z) - \log q_{\theta}(z) ]
\end{align}
$$
可以看到,不等号右边的期望里,一个是近似结果$q_\theta(z)$,另一个是贝叶斯的分子、比较好算的联合概率分布$p(x,z)$,完全避开了最难算的$p(x)$。而且,虽然$p(x)$具体取值不知道,但是我们知道它是一个定值,所以不等号左边,如果KL散度越来越小了,那么两个分布越来越接近,反过来期望就越来越大。那么,我们的优化目标就可以从式子(1)中的最大化的KL散度,迁移到式子(2)的最大化不等号右边的下界。
这个最大化的意思就是,因为这个下界恒小于等于$\log p(x)$的真实值。那么,不断抬高这个下界,就能使得这个下界的值,逼近$\log p(x)$的真实值。这个下界也就是VAE等带“变分”二字的方法中常说的ELBO(证据下界,Evidence Lower Bound),这个“证据”就指的是$p(x)$,因为它反映了观测数据的真实分布。
示例 Example
假定一个标量形式的隐式状态$z$的先验概率分布$p(z)$为:
$$
p(z) = \mathrm{e}^{-z}\cdot \mathrm{I}(z\geq 0) = \left\{
\begin{aligned}
&\mathrm{e}^{-z} &z\geq 0 \cr
&0 &z<0 \cr
\end{aligned}
\right.
$$
给定隐式状态取值为$z$时,观测值$x$的条件概率$p(x|z)$为高斯分布:
$$
\begin{align}
p(x|z) = & \ \mathcal{N}(x; \mu=z, \sigma=1) \nonumber \\
= & \ \frac{1}{\sqrt{2\pi}}\mathrm{e}^{(-\frac{1}{2}(x-z)^2)} \nonumber \\
\end{align}
$$
那么,可以计算出联合分布$p(x, z)$,以及进一步对联合分布中的所有隐式状态$z$积分,得到的观测值$x$的先验概率分布$p(x)$
$$
\begin{align}
p(x, z) = & \ p(x|z)p(z) \nonumber \\
= & \ \frac{1}{\sqrt{2\pi}}\mathrm{e}^{(-\frac{1}{2}(x-z)^2)} \cdot \mathrm{e}^{-z}\cdot \mathrm{I}(z\geq 0) \nonumber \\
\end{align}
$$
$$
\begin{align}
p(x) = & \ \int_0^\infty p(x, z) dz \nonumber \\
= & \ \int_0^\infty \frac{1}{\sqrt{2\pi}}\mathrm{e}^{(-\frac{1}{2}(x-z)^2)} \cdot \mathrm{e}^{-z}\cdot \mathrm{I}(z\geq 0) dz \nonumber \\
\end{align}
$$
可以看到,联合分布$p(x, z)$本身是两个指数函数的乘积,可以正常地算出函数值。但是对其在$[0, \infty)$(也就是$z\geq 0$)上算积分,事实上是非常难算的。而实践中大部分场景就是若干个指数函数(或者带有指数函数的高斯分布)组合成的,只能通过数值解法插值出来,也就是上面视频截图里的红线部分。
那么,基于上一章节描述的变分推断,是否能比较好地解这个问题(也就是近似后验概率$p(z|x)$)呢?首先,我们给出一个简单的参数化概率分布$q_\theta(z)$:
$$
q_\theta(z) = \theta\mathrm{e}^{-\theta z}\cdot \mathrm{I}(z\geq 0) = \left\{
\begin{aligned}
& \theta \mathrm{e}^{-\theta z} &z\geq 0 \cr
&0 &z<0 \cr
\end{aligned}
\right.
$$
计算前述式子(2)里的ELBO,记作$\mathcal{L}_q$:
$$
\begin{align}
\mathcal{L}_q = & \ \mathbb{E}_{z\sim q} [ \log p(x, z) - \log q_{\theta}(z) ] \nonumber \\
= & \ \mathbb{E}_{z\sim q} [ \log \frac{1}{\sqrt{2\pi}}\mathrm{e}^{(-\frac{1}{2}(x-z)^2)} \cdot \mathrm{e}^{-z}\cdot \mathrm{I}(z\geq 0) \nonumber \\
& - \log \theta\mathrm{e}^{-\theta z}\cdot \mathrm{I}(z\geq 0) ] \nonumber \\
\end{align}
$$
由于$\log (\cdot)$函数的定义域就是$(0, \infty)$,同时$\mathrm{I}(z\geq 0)$表示$z<0$时取$0$作为加权,导致代入$\log (\cdot)$无意义,所以可以直接舍去。将指数函数$\mathrm{e}^{(\cdot)}$与$\log(\cdot)$抵消,并整理与$z$和$\theta$无关的项为常数$\mathrm{C}$后,得到:
$$
\mathcal{L}_q = \mathbb{E}_{z\sim q} [ -\frac{1}{2}z^2 + (x - 1 + \theta)z - \log \theta + \mathrm{C} ]
$$
对带参数$\theta$的指数分布$q$求期望,有$\mathbb{E}_\theta [z^n] = \frac{n!}{\theta^n}$,则上式中的$z^2$和$z$项目均可以代入该期望公式。同时,$\log \theta$与$z$无关,对其求期望的结果还是本身:
$$
\mathcal{L}_q = - \frac{1}{\theta^2} + \frac{x-1+\theta}{\theta} - \log \theta + \mathrm{C}
$$
上式就是化简后的ELBO,为了求这个ELBO最大化时的参数$\theta$,令导数$\frac{\partial \mathcal{L}_q}{\partial \theta}=0$,代入$x=1.5$:
$$
\frac{\partial \mathcal{L}_q}{\partial \theta} = \frac{2}{\theta^3} - \frac{0.5}{\theta^2} + \frac{1}{\theta} = 0
$$
计算得到方程的解是$\theta=1.186$。将该参数代入$q_\theta(z)$,可以画出绿色曲线如下图所示:
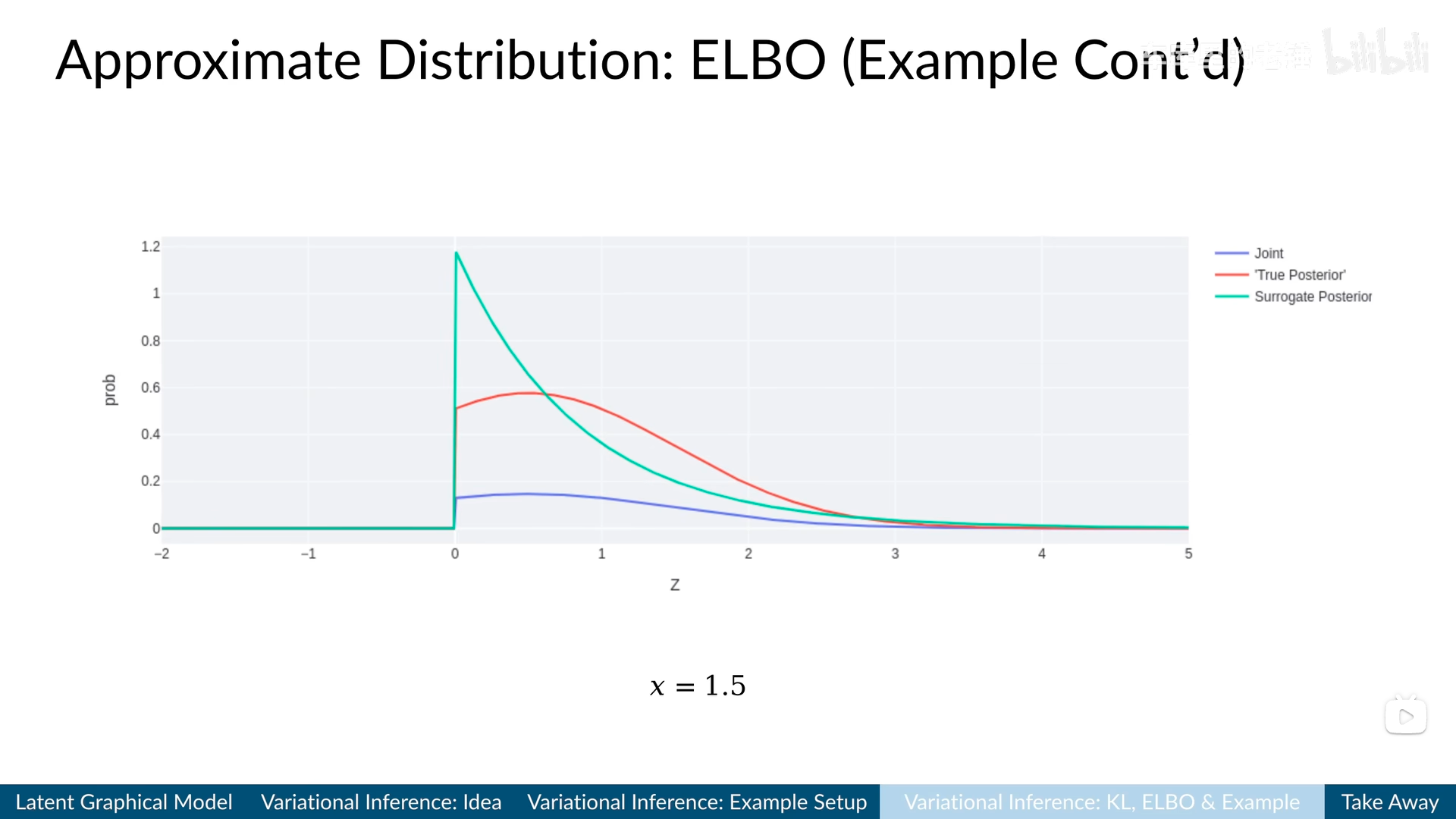
以及变分推理后得到的绿线$q_\theta(z)$。视频截图来自B站[1]
一方面,可以看到虽然绿色的曲线比蓝色的(联合分布)稍微好点了,但是距离红色(真实的后验概率)还是很远,说明$q_\theta(z)$的构造和选取很影响最终结果,而且这也只是一个观测数据点$x=1.5$的解,需要遍历所有数据点,每个样本优化出一个参数$\theta_x$,数据集无限大则参数无限大,拟合成本高且不实用。
从均摊分析(Amortized Analysis)的角度上考虑,机器学习、神经网络等学习方法可以有$\mathrm{K}$个全局参数,在训练过程中联合调整,与数据集规模无关,这样就能得到有限个参数,且训练结束后即可直接应用到测试集上。
另一方面,即使是标量形式的隐式状态$z$和观测值$x$都如此地难近似,更不要说高维的数据了,此时就需要机器学习、神经网络等学习方法,用更大规模的参数$\theta$在高维数据上学习拟合到更好的函数$q_\theta(z)$。
在VAE中的变体 Variant in VAE
首先,需要强调的一点是,Neural ODE[3]作为2018年的理论三大会NeurIPS的Best Paper,肯定是有其基本理论的,其中之一就是VAE。因此,它的底层学习机制还是一个生成式的模型,因为它的大部分任务是对时间序列的内插和外推,所以需要基于学习到的隐式状态,生成新的数据。
而前面描述的变分推断还是一个判别式的模型,粗浅一点讲,判别式模型是$x\rightarrow z$,而生成式模型是$z\rightarrow x$。但是从因果图来说,都是$z\rightarrow x$,因为这是数据产生的方式,要先有客观状态(物体就是类别A),才能有相应的观测(类别A的图片),生成式模型尝试模拟这个过程,判别式模型倒推反演这个过程。
那么是否有判别式的模型,帮助我们直接从观测数据倒推出内部的隐式状态呢?其实是有的,之后的记录中会详细对比,这里先讲基础的VAE和Neural ODE(而且Neural ODE真的不能有判别任务吗?也不尽然,其实原文里面有对应实验)。
这里参考B站视频[2],VAE的编码器Encoder是$q_\phi(z|x)$,给定输入数据求解隐式状态,生成器Decoder是$p_\theta(x|z)$,给定隐式状态求解生成数据,同时先验概率$p(x)$仍然是难求解的项目。同时,为了继承原有的变分性质,有别于普通自编码器(Auto-Encoder)输出了纯黑盒的中间隐式向量$z$,$q_\phi(z|x)$对于每个样本都输出$\mu_\phi(x)$和$\sigma_\phi(x)$,作为用于近似后验概率$p(z|x)$的高斯分布函数的参数。
同样,从均摊分析的角度考虑,如果ELBO使用式子(2)里的$q_\theta(z)$,每个样本仍然是要都学习一个$\theta_x$。因此,直接引入编码器$q_\phi(z|x)$,包含全局的参数$\phi$。重新构造ELBO($\mathcal{L}_q$)如下所示:
$$
\begin{align}
\mathcal{L}_q = & \ \mathbb{E}_{z\sim q} [ \log p(x, z) - \log q_{\phi}(z|x)] \nonumber \\
= & \ \mathbb{E}_{z\sim q} [ \log p_\theta(x|z)p(z) - \log q_{\phi}(z|x) ] \nonumber \\
= & \ \mathbb{E}_{z\sim q} [ \log p_\theta(x|z) + \log p(z) - \log q_{\phi}(z|x) ] \nonumber \\
= & \ \mathbb{E}_{z\sim q} [ \log p_\theta(x|z) - \log \frac{q_{\phi}(z|x)}{p(z)} ] \nonumber \\
= & \ \mathbb{E}_{z\sim q} [ \log p_\theta(x|z) ] - D(q_{\phi}(z|x)||p(z)) \\
\end{align}
$$
在式子(3)中,可以看到最终的两项分别对应了生成器和编码器:1)第一项$\mathbb{E}_{z\sim q} [ \log p_\theta(x|z) ]$的意思是,给定隐式向量$z$,生成器重构出真实观测值$x$的概率应当最大,重构出其他无关观测值的概率应当最小(因为我们是最大化ELBO),注意是采若干个$z\sim q$,对应若干个$x$,算期望;2)第二项$- D(q_{\phi}(z|x)||p(z))$,其实就是最小化KL散度$D(q_{\phi}(z|x)||p(z))$,也就是给定观测值$x$,编码器的编码的隐式向量$z$应当服从其先验概率分布$p(z)$。
与$p(x)$不同,隐式向量$z$是编码器学出来的,因此其概率分布可以预设。而$p(x)$是与数据观测值$x$有关,是一个自然分布,无法进行有效的预设,只能尝试拟合。因此,可以将先验概率分布设为标准高斯分布$\mathcal{N}(0, \mathrm{I})$。
当然,仔细看过的学习者会发现:不对啊,根据前面变分推断的分析,我最初设立$q_\phi(z|x)$的初衷是去拟合后验概率分布$p(z|x)$的,怎么这里又要去与一个先验概率分布$p(z)$拉近呢,这不是矛盾了吗?事实上,在一些场景里面,这会引发“后验塌陷”问题,也就是在学习过程中,$q_\phi(z|x)$过于接近先验分布$p(z)$,而不接近真实的后验分布$p(z|x)$。相当于直接将观测样本“死记硬背”,映射到标准高斯分布$\mathcal{N}(0, \mathrm{I})$里面,至于编码就不怎么学了。
这种情况可以通过多种方式解决:1)修改ELBO的优化目标,既然ELBO有两项,就可以调整加权,例如$\beta$-VAE使用$\beta>1$来鼓励模型更多地使用隐式状态$z$,而不是直接去$p(z)$里映射[4];2)修改先验分布,防止过拟合;3)修改模型架构,例如递归VAE[5]。
重参数化技巧 Reparameterization
对于式子(3)的ELBO,将其转换为编码器和解码器的损失函数。对于编码器对应的KL散度项,由于两者都是高斯函数:1)基于给定观测数据$x$,编码器预测了高斯函数的均值方差参数$q_\phi(z|x) = \mathcal{N}(z;\mu_\phi(x), \mathrm{\Sigma}_\phi(x))$,2)先验概率分布是标准高斯$q(z)=\mathcal{N}(z; 0, \mathrm{I})$。所以,直接代入高斯函数的KL散度公式:
$$
\begin{align}
& D(\mathcal{N}(\mu_0, \mathrm{\Sigma}_0) || \mathcal{N}(\mu_1, \mathrm{\Sigma}_1)) \nonumber \\
& = \frac{1}{2}(\mathrm{tr}(\mathrm{\Sigma_1}^{-1}\mathrm{\Sigma_0}) + (\mu_1 - \mu_0)^\top\mathrm{\Sigma_1^{-1}}(\mu_1-\mu_0) \nonumber \\
& - \mathrm{K} + \log \frac{\mathrm{det}\mathrm{\Sigma_1}}{\mathrm{det}\mathrm{\Sigma_0}}) \nonumber \\
\end{align}
$$
$$
\begin{align}
& D(q_\phi(z|x)||p(z)) = \frac{1}{2}(\mathrm{tr}(\mathrm{\Sigma_\phi(x)}) + \mu_\phi(x)^\top\mu_\phi(x) \nonumber \\
& - \mathrm{K} + \log (\mathrm{det}\mathrm{\Sigma_\phi(x)})) \nonumber \\
\end{align}
$$
其中,$\mathrm{K}$是隐式向量$z$的维度大小。不得不说,这公式具体怎么来的,我也没推导过。可以看到式子可微,通过反向传播能更新参数,问题不大。
对于解码器对应的最大化重建项,将重建结果的概率$p_\theta(x|z)$也建模为一个高斯分布$p_\theta(x|z) = \mathcal{N}(x; \mu_\theta(z), \sigma^2\mathrm{I})$,$\sigma$为定值,这样求$\log (\cdot)$之后,有:
$$
\log p_\theta(x|z) = -\mathrm{C}\Vert x-\mu_\theta(z) \Vert^2 + \mathrm{D}
$$
其中,$\mathrm{C}$和$\mathrm{D}$都是与$\theta$无关的常数项。因此,在后续反向传播求梯度时,只需要求解$\nabla_\theta \Vert x-\mu_\theta(z) \Vert^2$,就是真实观测值$x$与基于$z$的重建结果$\mu_\phi(z)$算L2-范数。但是,真正的最大化重建项是一个期望$\mathbb{E}_{z\sim q_\phi} [ \log p_\theta(x|z) ]$,需要在编码器预测的高斯分布$q_\phi(z|x) = \mathcal{N}(z;\mu_\phi(x), \mathrm{\Sigma}_\phi(x))$上多次采样,这个多次前向采样的过程,是无法通过反向传播,从而一路更新到编码器这边(相当于是要根据解码器输出的均值方差$\mu_\phi(x)$,$\mathrm{\Sigma}_\phi(x)$,新建一个高斯分布)。
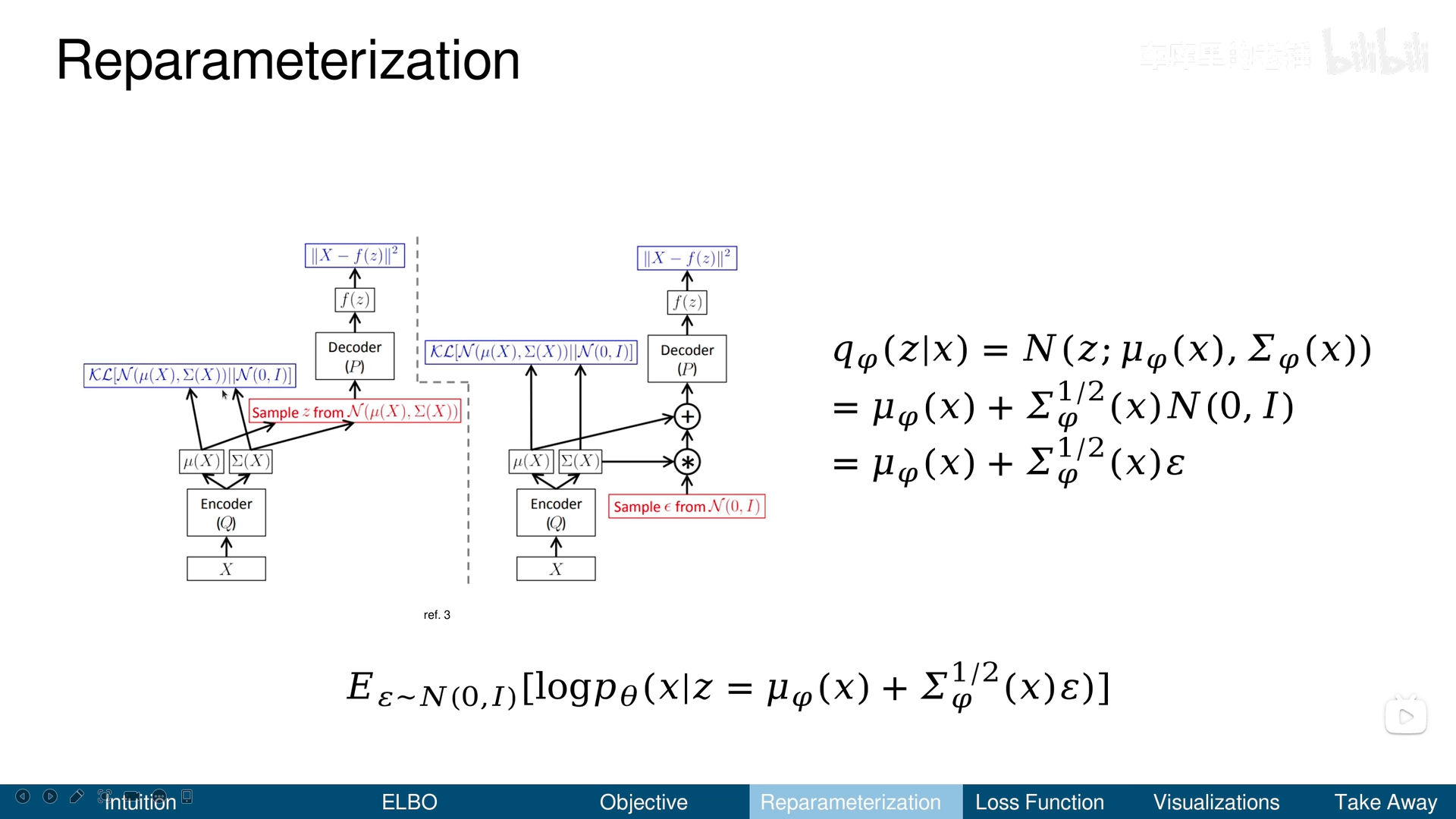
可以看到重参数之后,编码器预测的均值方差$\mu_\phi(x)$,$\mathrm{\Sigma}_\phi(x)$,能够收到梯度。视频截图来自B站[2]
那么就需要避免这种新建高斯分布进行随机采样的操作。如上图的右半图所示,重参数技巧选择在一个标准高斯分布上采样,然后让采样的结果与编码器预测的均值方差$\mu_\phi(x)$,$\mathrm{\Sigma}_\phi(x)$,进行线性变换,从而得到与直接在编码器输出的高斯分布上采样等效的结果,还能传梯度到编码器(黑框和黑线)。
在Neural ODE中的应用 Application in Neural ODE
想要了解VAE在Neural ODE中的应用,最直观的肯定是看pipeline和学习目标ELBO。很巧的是,陈天琦团队在2019年NeurIPS发表的Neural ODE续作Latent ODE[6]中,应该是作者们特别设计了排版,让pipeline和学习目标放在了同一页相邻的地方。这篇文章其实和Neural ODE也就左半边编码器Encoder不一样(一个是RNN,一个是ODE-RNN),所以我们直接看Latent ODE的图:

可以看到,这个ELBO式子(9)可以说是和前面的式子(3)一模一样,也是对生成器(ODESolve的红色部分)最大化重构项,以及最小化编码器(ODE-RNN的绿色部分)输出的高斯分布(图正中间的$\mu$和$\sigma$)与先验分布的KL散度。
但是需要注意的是,这也继承了VAE的任务特性:一方面,训练的过程是自监督的,观测数据既作为输入,也作为重构目标,如果观测数据的数量以及内容偏少,学习的实际效果是难以保证的(例如直接观测数据点太少的情况);另一方面,隐式状态的表达形式是高斯分布的参数,虽然它相比于自编码的黑盒向量更加显式,但还不是我们想要的与客观世界对应的、结构化的内在状态(例如类别、阶段、变化等)。
而且,这也并不是Neural ODE的特殊之处,把左右两边的编解码器,全部换成RNN或者Transformer,其实也能对时序数据的隐式状态进行建模。而Neural ODE真正的优势,简而言之,正是Latent ODE的标题:不均匀采样的时间序列,而这就要等到下次笔记了。
参考资料
- [1] 车库里的老锤.【15分钟】了解变分推理. https://www.bilibili.com/video/BV1Gs4y157BU
- [2] 车库里的老锤.【15分钟】了解变分自编码器. https://www.bilibili.com/video/BV1Ns4y1J7tK
- [3] Chen R T Q, Rubanova Y, Bettencourt J, et al. Neural ordinary differential equations[J]. Advances in neural information processing systems, 2018, 31.
- [4] Higgins I, Matthey L, Pal A, et al. beta-vae: Learning basic visual concepts with a constrained variational framework[C]//International conference on learning representations. 2016.
- [5] Kim M, Pavlovic V. Recursive inference for variational autoencoders[J]. Advances in Neural Information Processing Systems, 2020, 33: 19632-19641.
- [6] Rubanova Y, Chen R T Q, Duvenaud D K. Latent ordinary differential equations for irregularly-sampled time series[J]. Advances in neural information processing systems, 2019, 32.
感谢阅读!在2023年的最后一天,终于写好了这篇笔记!
也是时隔多年,再次在博客里发一篇技术文章,令人万分感慨。
如有意见和建议,欢迎通过首页的联系方式联系作者。
本文参考资料均来源于网络,作者保留相关权利,转载请注明出处。