本文是学习Neural ODE过程中的第二篇个人笔记
主要是ODE的基本原理,包括前向计算过程,以及基于伴随方法的反向传播
同时会简要地提一下State Estimation状态估计,其余论文细节以及SDE会在下一次记录。
常微分方程 Ordinary Differential Equation
常微分方程指的是自变量只有一个的微分方程,在这里一般表示的是时间$t$,若有多个自变量则为偏微分方程。设因变量为$y$,两者的变化关系$f(y, t)$可以用常微分方程表示:
$$
\begin{equation}
dy = f(y, t)dt
\end{equation}
$$
为了得到某一个时刻$\mathrm{T}$上的$y_\mathrm{T}$具体值, 对式子(1)在$[0, \mathrm{T}]$上求定积分:
$$
\begin{equation}
y_\mathrm{T} = y_0 + \int_0^\mathrm{T} f(y, t)dt
\end{equation}
$$
其中,$y_0$为$y$在$t=0$时刻的初始值。显然,如果没有这个初始值$y_0$,式子(2)的积分项只是起止时刻的$y$的总变化量,也就是$\Delta y=y_\mathrm{T}-y_0$。因此,可以称这种问题为初值问题(IVP,Initial Value Problem)。
常微分方程的求解器 ODE Solver
对于$f(y,t)$,如果它是一些简单的函数,则可以直接求解得到积分的解析解。然而,当它过于复杂而无法求解积分时,需要用数值计算的方法来近似计算其积分值,记为求解器$\mathrm{ODESolver}$,则式子(2)可以改写为:
$$
y_\mathrm{T} = \mathrm{ODESolver}(y_0, f, [0, \mathrm{T}])
$$
最简单的$\mathrm{ODESolver}$是欧拉方法(Euler’s Method)。设在自变量轴$t$上的固定步长$h$,从初始时间$t_0=0$到下一步长时间$t_1=t_0+h$段内,为了知道$t_1$上具体的$y$值是多少,需要和式子(2)一样求积分,但是过于复杂没办法求解析解。
由于$f(y, t)$表示的是$y$随$t$的变化量,也就是导数,则可以求出在初始时间$t_0$对应的初值$y_0$上的导数$f(y_0, t_0)$。那么,根据导数的性质,将该导数作为斜率(Slope),乘以自变量轴上$t$的变化量,也就是步长$h$,可以得到因变量轴$y$上经过该步长的变化量$h \ f(y_0, t_0)$。将这个变化量加上初值,则为下一步长时间的因变量值$y_1$(的近似值):
$$
y_1 = y_0 + h \ f(y_0, t_0)
$$
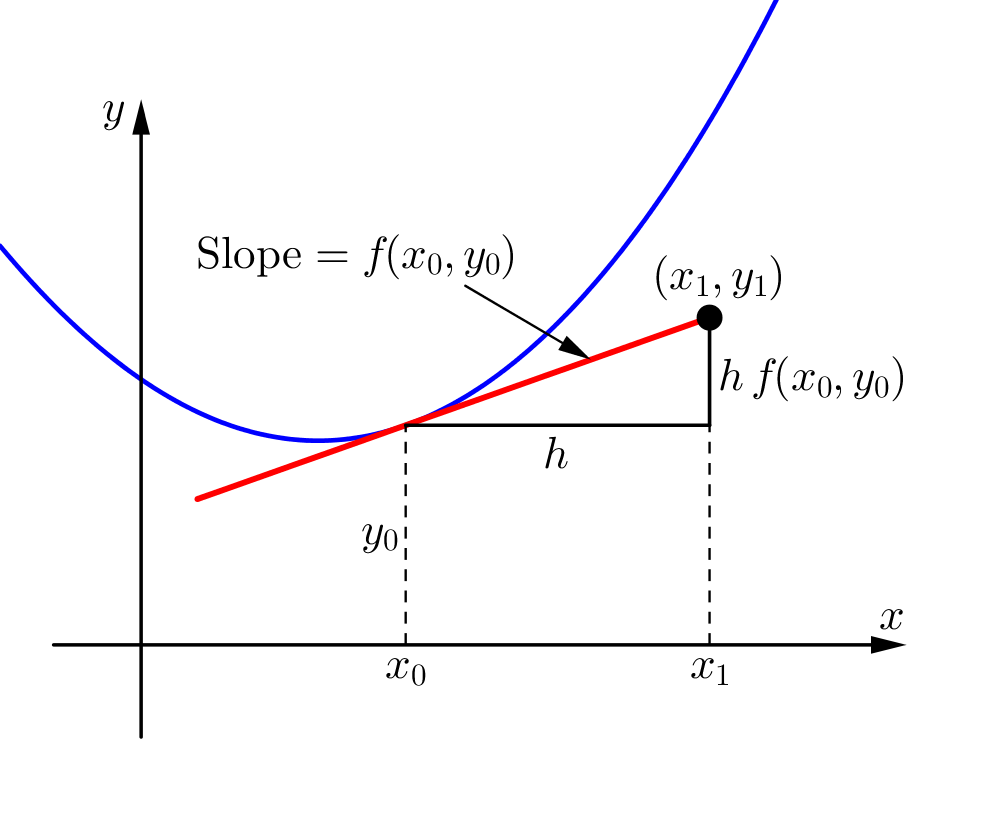
在得到了下一对自变量和因变量$(t_1, y_1)^\top$后,继续取$f(y_1, t_1)$计算$y_2$。如此迭代,则可以算到$y_\mathrm{T}$,但是该解析解一定会和真实值有一定的误差,因为这种计算方法基于步长$h$和斜率$f(x_t, y_t)$构成的三角形,而不是平滑变化过程。
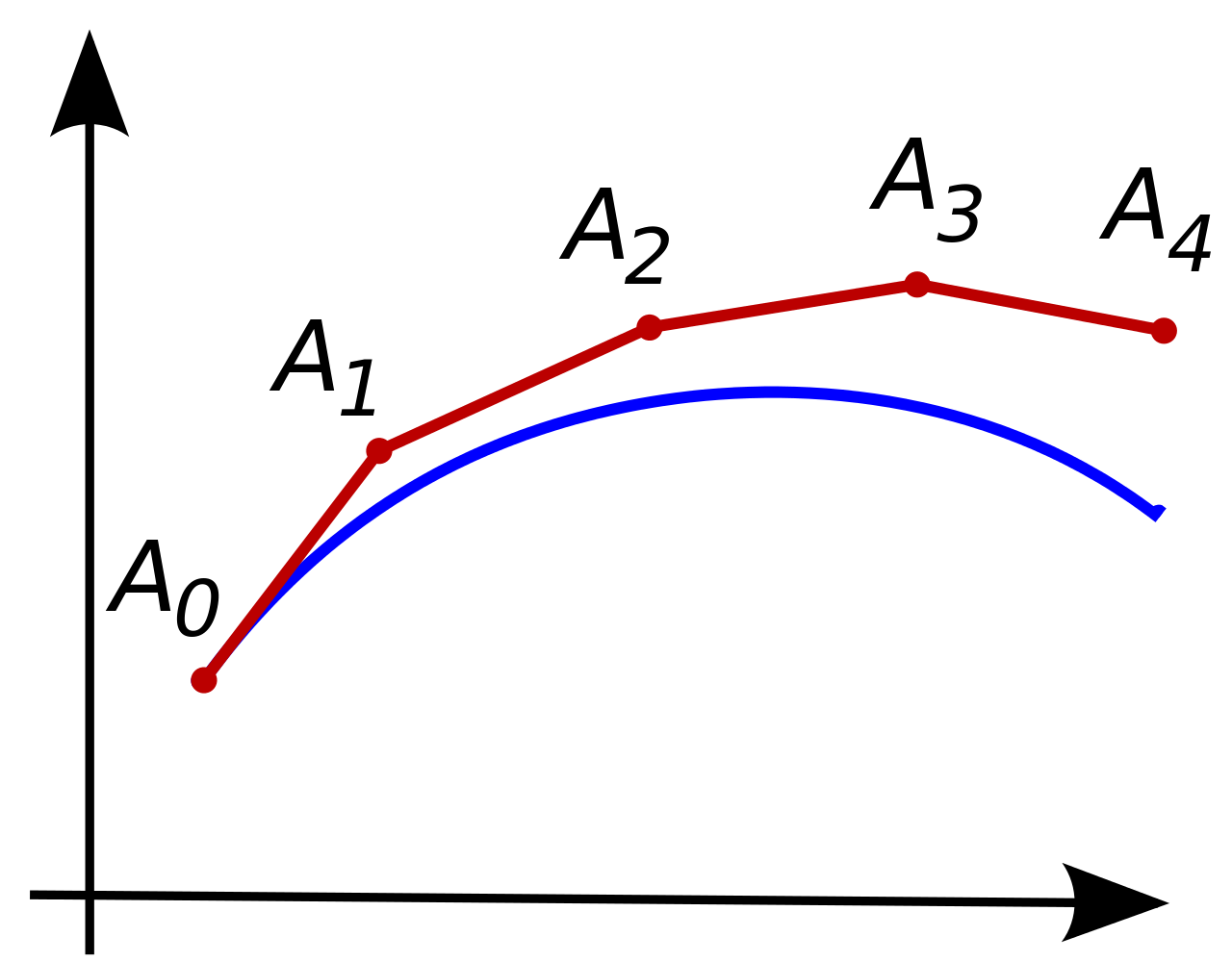
但是,随着步长$h$的逐渐减小,欧拉方法计算过程的轨迹也会和真实函数越来越近,可以参见维基百科[2]给出的示例。值得注意的是,这一计算过程不仅能够得到$y_\mathrm{T}$本身,也能将过程中若干个中间结果$y_t$连起来,可视化$y$的变化过程。
神经常微分方程 Neural ODE
回顾上一节,常微分方程求解器的前提条件是,已知变化关系函数$f(y,t)$的具体形式,且$f(y,t)$的积分难求解析解。但在实际应用中,还有更多只知道若干个$(t, y_t)^\top$的数据点(可能均匀采样,也可能不均采样),不知道$f(y,t)$具体形式的情况。那么,如何通过学习的方式,拟合出$f(y,t)$后,再使用$\mathrm{ODESolver}$求解$y_\mathrm{T}$呢?
在讲2018年理论三大会NeurIPS的Best Paper、陈天琦团队发表的Neural ODE[3]之前,我们需要回顾一个更加熟悉的工作,也就是已经成为CV界著名的基础设施、大佬何凯明团队在CV三大会CVPR 2016上发表的ResNet[4]。
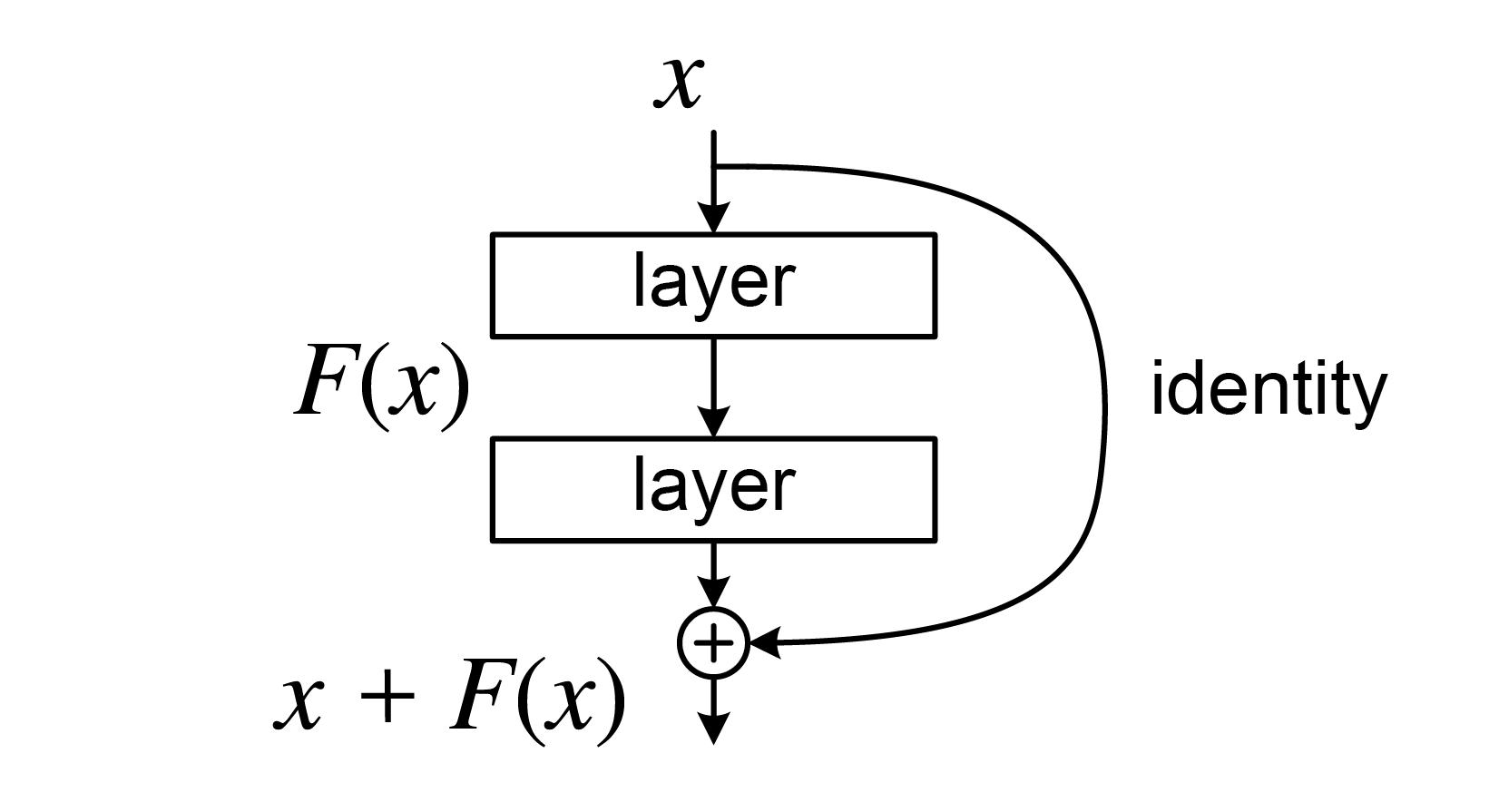
对于ResNet中的第$t$个Residual Block,其输入的隐式特征为$x_t$,处理该特征的网络参数为$\theta_t$,输出的隐式特征为$x_{t+1}$,则该Residual Block输入输出隐式特征的过程,可以用公式表示为:
$$
x_{t+1} = x_t + f(x_t, \theta_t)
$$
由于Resisual Block的个数一般是整数个,则步长$h=1$。当步长大小趋近于0,也即$h \rightarrow 0$时,有:
$$
\begin{align}
& x_{t+1} = x_t + f(x_t, \theta_t) \nonumber \\
& \Rightarrow \frac{x_{t+1} - x_t}{1} = f(x_t, \theta_t) \nonumber \\
& \Rightarrow \frac{x_{t+h} - x_t}{h} = f(x_t, \theta_t) \nonumber \\
& \Rightarrow \lim_{h \rightarrow 0} \frac{x_{t+h} - x_t}{h} = f(x_t, t, \theta) \nonumber \\
& \Rightarrow \frac{dx_t}{dt} = f(x_t, t, \theta) \\
\end{align}
$$
其中,在转换为极限时,Residual Block $f(x_t, \theta_t)$需要改成$f(x_t, t, \theta)$。因为当步长$h \rightarrow 0$时,需要无数个$\theta_t$进行迭代,参数总量趋于无穷,无法实际应用。转为固定参数$\theta$后,$t$可以提示网络要输出对应时间下的结果。
所以,如式子(3)所示,ResNet作为一个神经网络,同样可以表示为常微分方程ODE的形式。当然,也可以从式子(3)中对步长(从步长为固定整数1、迭代次数也是固定的,到步长趋于0、迭代次数趋于无穷)、网络参数(从每次迭代使用不同的网络参数,到所有迭代共享一个网络参数且用$t$提示网络当前迭代时间)的修改看出,原始的ResNet并不能表示常微分方程,需要进行一定的改造。
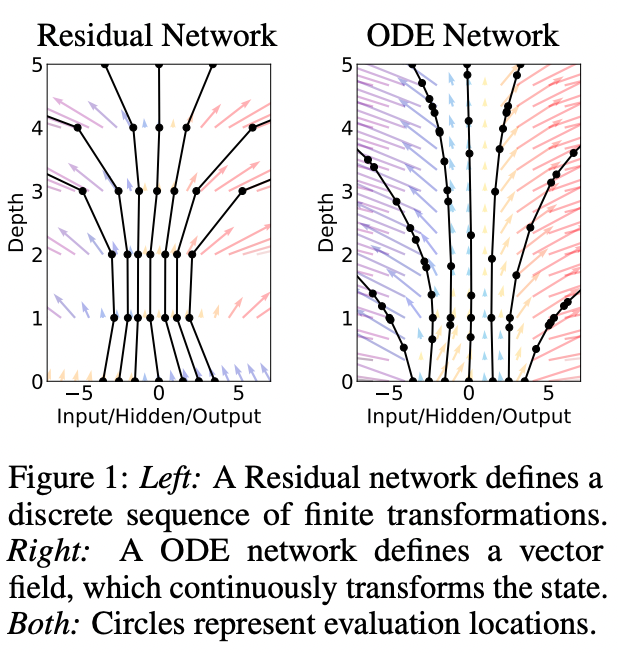
在Neural ODE原文[3]的首图中,可以更直观地看出两者的区别。纵轴为网络深度,可以视为自变量轴$t$;横轴为输入、输出和隐式特征,可以视为因变量$x$或$y$。左图是ResNet,时间$t$的步长为固定整数1,每一次$x$都只能从上一个步长变化到下一个,变化过程是离散的,只能拿这些因变量作为验证点(图中黑色实心圆点,evaluation locations);右图图是Neural ODE,时间$t$的步长为无穷小,可以近似为连续过程,任意不均匀的时间点都可以计算$x$,作为验证点。
同样的,对于循环神经网络RNN,虽然与ResNet的网络参数使用方式不同,所有迭代共享一个网络参数,但也无法迭代非整数个步长。上图没有考虑网络参数是否共享的问题,因此RNN也一样只能输出类似于左侧的结果。
因此,Neural ODE能够直接在不知道$f(y,t)$具体形式的情况,基于若干个$(t, y_t)^\top$的数据点作为训练集,用网络参数$\theta$拟合出一个神经网络形式的ODE,也就是$f(y_t, t, \theta)$,然后再将这一形式代入到$\mathrm{ODESolver}$中,求解出需要的$y_\mathrm{T}$值。
伴随方法 Adjoint Method
那么,如何训练出一个Neural ODE呢?最自然的方式,肯定是在某一点有真实值$(t_1, y_t)^\top$时,将其与Neural ODE的输出$\hat{y_t}$计算损失并反向传播梯度。但是,从上述Neural ODE的性质可以看出,它的迭代步长远小于ResNet、RNN的整数步长,前向输出$\hat{y_t}$所经历的迭代次数也非常多(例如$10^2\sim 10^3$次)。如果直接建立梯度的计算图,将需要保存大量的前向和反向的中间特征和中间梯度,消耗大量资源。因此,Neural ODE原文采用了伴随方法(Adjoint Method)。这里参考这篇知乎文章的推导过程[5]。
首先,需要注意的是,Neural ODE并未直接对预测值$\hat{y_t}$使用式子(3)进行ODE方式的更新,而是和ResNet、RNN一样,对隐式特征进行更新。然后通过另一个神经网络,输入隐式特征,输出预测值。这里为了和原文保持一致,将隐式特征记作$z(t)$。省略输出预测值、预测值与真实值计算损失的过程,将损失函数$\mathcal{L}$记为隐式特征的函数$\mathcal{L}(z(t))$:
$$
\begin{align}
\mathcal{L}(z(t_1)) & = \mathcal{L}(\mathrm{ODESolver}(z(t_0), f, t_0, t_1, \theta)) \nonumber \\
& = \mathcal{L}(z(t_0) + \int_{t_0}^{t_1} f(z(t), t, \theta)dt) \nonumber \\
\end{align}
$$
由链式法则,在任意时刻$t \leq t_1$(因为是反向传播,从最终的$t_1$算梯度往回传),对于损失函数求隐式特征偏导:
$$
\frac{\partial \mathcal{L}}{\partial z(t)} = \frac{\partial \mathcal{L}}{\partial z(t_1)} \frac{\partial z(t_1)}{\partial z(t)}
$$
定义一个伴随状态(Adjoint State),与时间$t$相关的函数$a(t)$:
$$
\begin{equation}
a(t) = \frac{\partial \mathcal{L}}{\partial z(t)}
\end{equation}
$$
那么对于任意$t+\epsilon > t$时刻(包括$t_1$在内),都有:
$$
\begin{align}
\frac{\partial \mathcal{L}}{\partial z(t)} & = \frac{\partial \mathcal{L}}{\partial z(t+\epsilon)} \frac{\partial z(t+\epsilon)}{\partial z(t)} \nonumber \\
& = a(t+\epsilon) \frac{\partial z(t+\epsilon)}{\partial z(t)} \\
\end{align}
$$
从$t$时刻开始,求解$t+\epsilon$时刻的隐式特征$z(t+\epsilon)$,可以算积分:
$$
\begin{equation}
z(t+\epsilon) = z(t) + \int_{t}^{t+\epsilon} f(z(t’), t’, \theta)dt’
\end{equation}
$$
将式子(4)、(6)代入式子(5),可以得到:
$$
\begin{align}
& a(t) = a(t+\epsilon) \frac{\partial}{\partial z(t)} ( z(t) + \int_{t}^{t+\epsilon} f(z(t’), t’, \theta)dt’) \nonumber \\
& = a(t+\epsilon) (1 + \frac{\partial}{\partial z(t)} (\int_{t}^{t+\epsilon} f(z(t’), t’, \theta)dt’)) \nonumber \\
& \Rightarrow a(t+\epsilon) - a(t) \nonumber \\
& = - a(t+\epsilon) \frac{\partial}{\partial z(t)} (\int_{t}^{t+\epsilon} f(z(t’), t’, \theta)dt’)
\end{align}
$$
式子(7)即可描述伴随方程$a(t)$随时间$t$的变化,进一步计算$\frac{da(t)}{dt}$:
$$
\begin{align}
& \frac{da(t)}{dt} = \lim_{\epsilon \rightarrow 0} \frac{a(t+\epsilon) - a(t)}{\epsilon} \nonumber \\
& = \lim_{\epsilon \rightarrow 0} \frac{- a(t+\epsilon) \frac{\partial}{\partial z(t)} (\int_{t}^{t+\epsilon} f(z(t’), t’, \theta)dt’)}{\epsilon} \nonumber \\
& = \lim_{\epsilon \rightarrow 0} \frac{- a(t+\epsilon) \frac{\partial}{\partial z(t)} (\epsilon \cdot f(z(t), t, \theta))}{\epsilon} \nonumber \\
& = \lim_{\epsilon \rightarrow 0} - a(t+\epsilon) \frac{\partial f(z(t), t, \theta)}{\partial z(t)} \nonumber \\
& = - a(t) \frac{\partial f(z(t), t, \theta)}{\partial z(t)} \\
\end{align}
$$
由于$\epsilon \rightarrow 0$,且偏导$\frac{\partial}{\partial z(t)}$与$\epsilon$无关。一个小区间的积分,就是高度为函数值,宽度为无穷小的矩形面积,则上式中的积分,就等于在$t$这个点上的$f$函数值乘以一个$dt’ = \epsilon$。分子分母两个$\epsilon$约去后,又由$\epsilon \rightarrow 0$,则$a(t+\epsilon) = a(t)$。
式子(8)就是伴随状态$a(t)=\frac{\partial \mathcal{L}}{\partial z(t)}$随时间的常微分方程,既然是常微分方程,就可以使用$\mathrm{ODESolver}$近似求解任意时刻的伴随状态,无需对偏导$\frac{\partial \mathcal{L}}{\partial z(t)}$本身建立复杂的反向传播计算图:
$$
\begin{align}
& a(t_0) = a(t_1) + \int_{t_1}^{t_0} \frac{da(t)}{dt} dt \nonumber \\
& = a(t_1) - \int_{t_1}^{t_0} a(t) \frac{\partial f(z(t), t, \theta)}{\partial z(t)} dt \nonumber \\
& = \mathrm{ODESolver}(a(t_1), - a(t) \frac{\partial f}{\partial z(t)}, t_1, t_0)
\end{align}
$$
但是,$\frac{\partial \mathcal{L}}{\partial z(t)}$只是反向传播的一部分,计算出这个损失函数与隐式特征的偏导之后,还要计算出损失函数与网络参数的偏导,也定为伴随状态$a_\theta(t) = \frac{\partial \mathcal{L}}{\partial \theta(t)}$。虽然,根据Neural ODE的性质,不同迭代次数下的网络参数$\theta$是不变的。但是,由于最终的梯度由$\geq 1$个不同真实值$(t, y_t)^\top$计算损失累积得到,所以认为仍然与时间有关,但是$\frac{\partial \theta}{\partial t} = 0$。由链式法则:
$$
\begin{align}
& a_\theta(t) = \frac{\partial \mathcal{L}}{\partial z(t+\epsilon)} \frac{\partial z(t+\epsilon)}{\partial \theta(t)} \nonumber \\
& + \frac{\partial \mathcal{L}}{\partial \theta(t+\epsilon)} \frac{\partial \theta(t+\epsilon)}{\theta(t)} \nonumber \\
& = a(t+\epsilon) \frac{\partial z(t+\epsilon)}{\partial \theta(t)} + a_\theta (t+\epsilon) \cdot 1 \\
& = a(t+\epsilon) \int_{t}^{t+\epsilon} \frac{\partial f}{\partial \theta} dt + a_\theta (t+\epsilon) \nonumber \\
& \Rightarrow a_\theta(t+\epsilon) - a_\theta(t) \nonumber \\
& = - a(t+\epsilon) \int_{t}^{t+\epsilon} \frac{\partial f}{\partial \theta} dt \\
\end{align}
$$
其中,式子(6)的$z(t+\epsilon)$积分可以代入到式子(10)中。式子(11)即可描述伴随方程$a_\theta(t)$随时间$t$的变化,进一步计算$\frac{da_\theta(t)}{dt}$:
$$
\begin{align}
& \frac{da_\theta(t)}{dt} = \lim_{\epsilon \rightarrow 0} \frac{a_\theta(t+\epsilon) - a_\theta(t)}{\epsilon} \nonumber \\
& = \lim_{\epsilon \rightarrow 0} \frac{- a(t+\epsilon) \int_{t}^{t+\epsilon} \frac{\partial f}{\partial \theta} dt}{\epsilon} \nonumber \\
& = - a(t) \frac{\partial f(z(t), t, \theta)}{\partial \theta(t)} \\
\end{align}
$$
过程与式子(8)相同,此处省略若干步骤。由此,式子(12)也是对伴随状态$a_\theta(t) = \frac{\partial \mathcal{L}}{\partial \theta(t)}$的常微分方程,也可以使用$\mathrm{ODESolver}$近似求解任意时刻的伴随状态,无需对$\frac{\partial \mathcal{L}}{\partial \theta(t)}$本身建立复杂的反向传播计算图,同式子(9):
$$
\begin{align}
& a_\theta(t_0) = a_\theta(t_1) + \int_{t_1}^{t_0} \frac{da_\theta(t)}{dt} dt \nonumber \\
& = a_\theta(t_1) - \int_{t_1}^{t_0} a(t) \frac{\partial f(z(t), t, \theta)}{\partial \theta} dt \nonumber \\
& = \mathrm{ODESolver}(a_\theta(t_1), - a(t) \frac{\partial f}{\partial \theta}, t_1, t_0)
\end{align}
$$
从式子(13)可以看到,由于$a_\theta(t)$依赖于$a(t)$的求解,$a(t)$又依赖于$z(t)$的求解,因此Neural ODE原文将它们同时送入同一个$\mathrm{ODESolver}$,从而进一步提高了计算效率。为了便于复用,Neural ODE的作者团队封装了这套特殊算法的代码库,作为他们开源项目的组成部分:torchdiffeq。

其中“aug_dynamics”相当于式子(3)、(9)和(13)的联立之后,互相代入现有值
图片来自Neural ODE论文原文[3]
有趣的是,可以注意到前面的时间全是$t_0$和$t_1$,而且是从$t_1$倒着回到$t_0$(这倒是好理解,因为是算梯度,肯定是从最后一次计算损失的时候往回传)。为什么不是整条预测序列呢(例如从$t_1$到$t_\mathrm{start}$)?如果这样的话,可以看到用上图中只有一个真实值$(t_1, y_{t_1})^\top$计算损失得到的$\frac{\partial \mathcal{L}}{\partial z(t_1)}$,忽略了从$t_1$到$t_\mathrm{start}$中间若干个其他通过真实值$(t, y_t)^\top$得到的$\frac{\partial \mathcal{L}}{\partial z(t_1)}$,这样会导致最终计算出的$\frac{\partial \mathcal{L}}{\partial z(t_0)}$有较大的误差。因此,Neural ODE原文只用上述算法计算真实值之间的伴随状态,遇到真实值就用真实值的$\frac{\partial \mathcal{L}}{\partial z(t_1)}$作为初始值,重新用上述算法计算,从而使得累积误差最小。
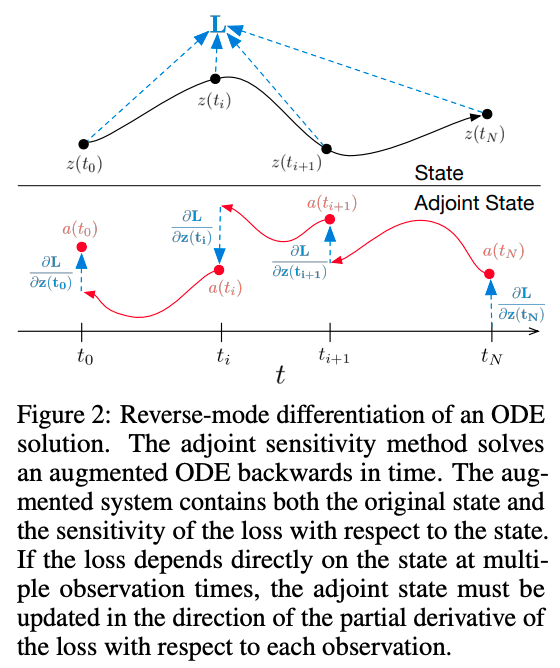
上图:先计算损失$\mathcal{L}$,得到真实的$\frac{\partial \mathcal{L}}{\partial z(t)}$。下图:红线是$\mathrm{ODESolver}$计算出来的伴随状态,蓝色虚线是基于真实的$\frac{\partial \mathcal{L}}{\partial z(t)}$来重新开始计算$a(t)$,从而使得误差累积更小。图片来自Neural ODE论文原文[3]
在状态估计中的应用 Application in State Estimation
从前文可以看到,Neural ODE的隐式特征(也可以称为隐式状态,Hidden State)实际上和ResNet、RNN一样,是黑盒化的特征向量或张量,实际上无法反应与客观世界对应的、结构化的内在状态,同时也很难直观地可视化。为了能够在一定程度上将这些隐式状态可视化,Kevin Course和Prasanth B. Nair在2023年10月的Nature正刊上发表了“State estimation of a physical system with unknown governing equations”[6]。
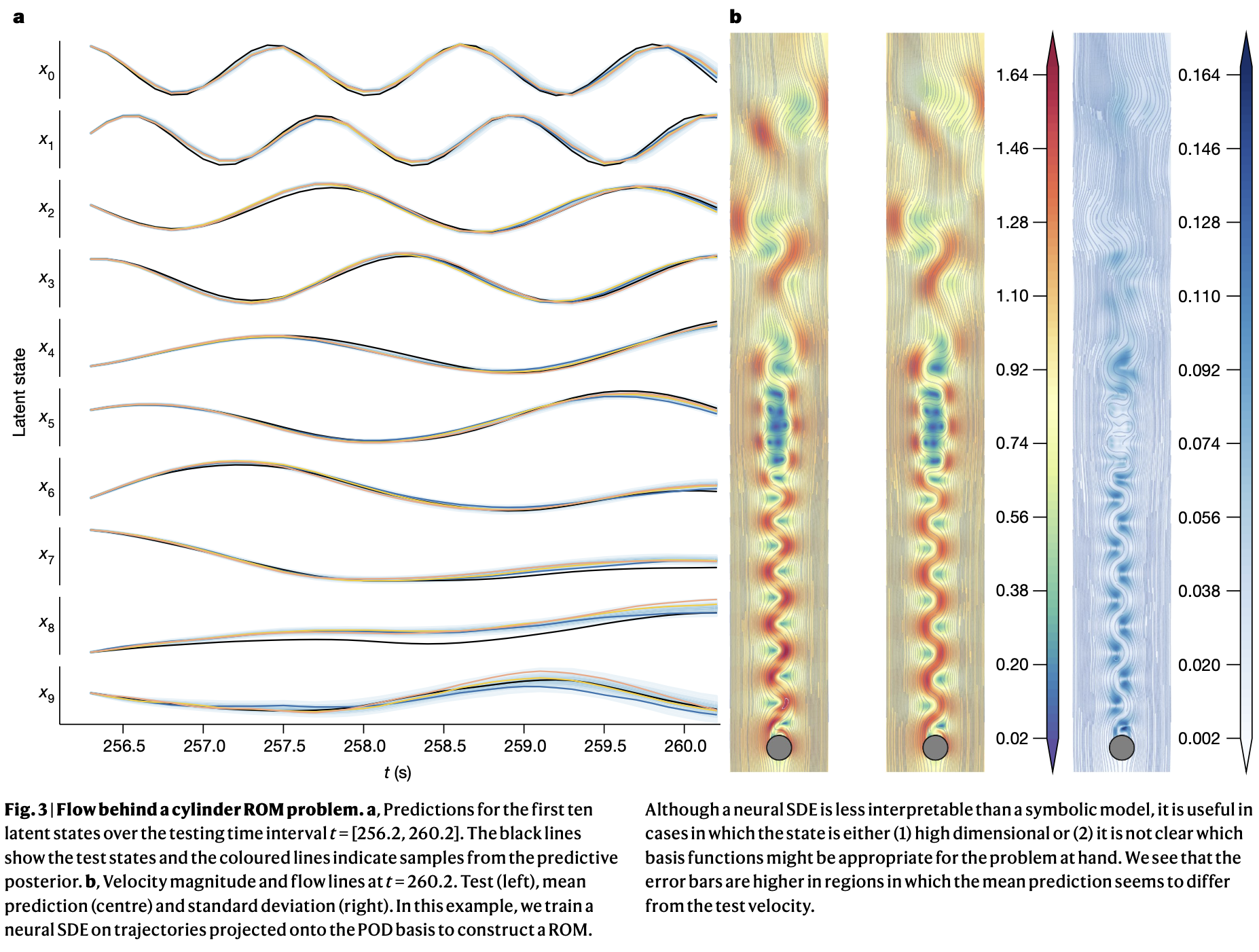
该工作采用了相比Neural ODE更加贴近真实物理系统、考虑了随机布朗运动的Neural SDE(SDE即随机微分方程,Stochastic Differential Equation),通过在有限的观测数据$y(t)$上学习,得到了更强的对$y(t)$进行内插和外推的能力,同时也学习到了更加可解释的隐式状态$x(t)$。
虽然,他们也认为,Neural SDE相比纯符号模型(通过建模方程、待定参数拟合的方式)可解释性更低,但是也可用于(1)无法用方程拟合的复杂高维数据,例如视频数据[7];(2)无法确定合适的基础方程用于建模和拟合的情况。至于这些工作如何实现状态估计的、以及相应的技术细节,就留到下次笔记。
参考资料
- [1] Euler's method. https://teaching.smp.uq.edu.au/scims/Appl_analysis/Eulers_method.html
- [2] Euler method. https://en.wikipedia.org/wiki/Euler_method
- [3] Chen R T Q, Rubanova Y, Bettencourt J, et al. Neural ordinary differential equations[J]. Advances in neural information processing systems, 2018, 31.
- [4] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.
- [5] Maple小七. 理解伴随法(Adjoint Method)在Neural ODE中的应用. https://zhuanlan.zhihu.com/p/337575425
- [6] Course K, Nair P B. State estimation of a physical system with unknown governing equations[J]. Nature, 2023, 622(7982): 261-267.
- [7] Course K, Nair P B. Amortized Reparametrization: Efficient and Scalable Variational Inference for Latent SDEs[C]//Thirty-seventh Conference on Neural Information Processing Systems. 2023.
感谢阅读!如有意见和建议,欢迎通过首页的联系方式联系作者。
本文参考资料均来源于网络,作者保留相关权利,转载请注明出处。