本文是学习Neural ODE过程中的第三篇个人笔记
主要是SDE的基本原理、高斯过程近似、重参数技巧和均摊分析
以及在状态估计中的应用,包括Kevin Course和Prasanth B. Nair在2023年Nature和NeurIPS上的论文。
勘误和一些推论 Corrigendum and Corollaries
首先需要更正一下,其实Neural ODE也支持直接用中间的隐式状态表示预测结果,不需要额外的网络来解码隐状态。可以参见陈天琦团队的github仓库[1]的简单示例。由于这个示例需要拟合的是下图螺旋运动轨迹方程,只有两个变量:运动点的2D坐标$x$和$y$,而且目标方程也不复杂,只有几个参数,所以直接让神经网络接受上一次输出的$(x, y)^\top$,再输出下一次的$(x, y)^\top$,不需要复杂的隐藏变量$z(t)$,也能正确拟合这个方程。
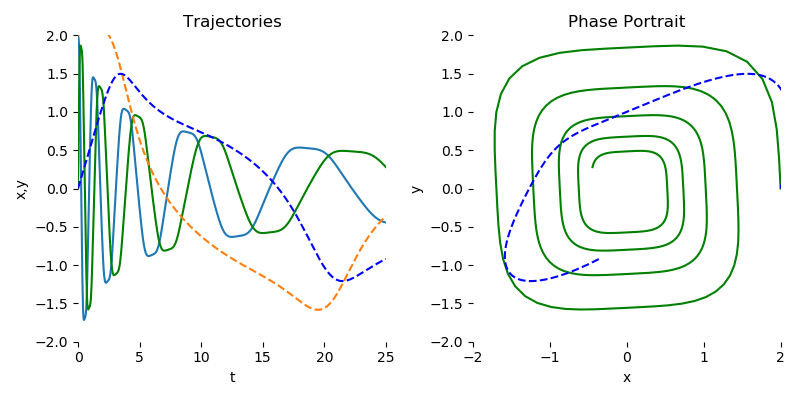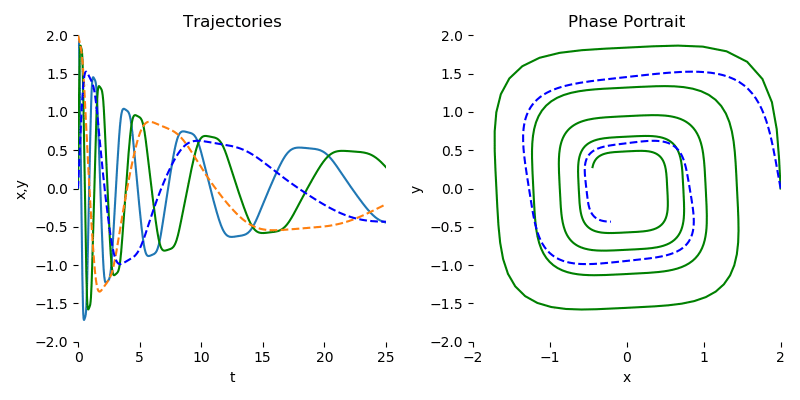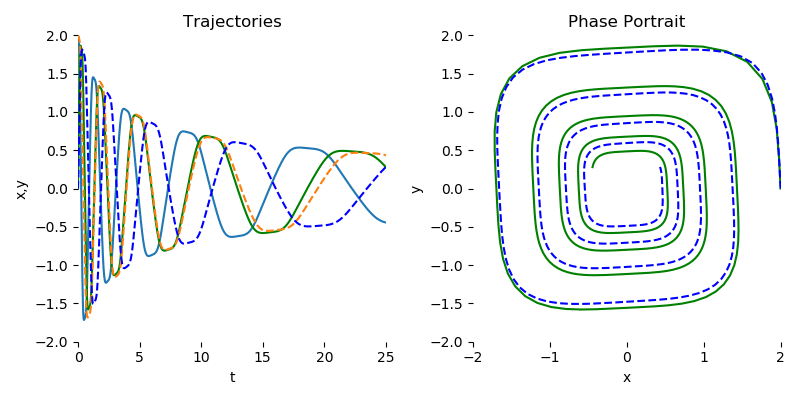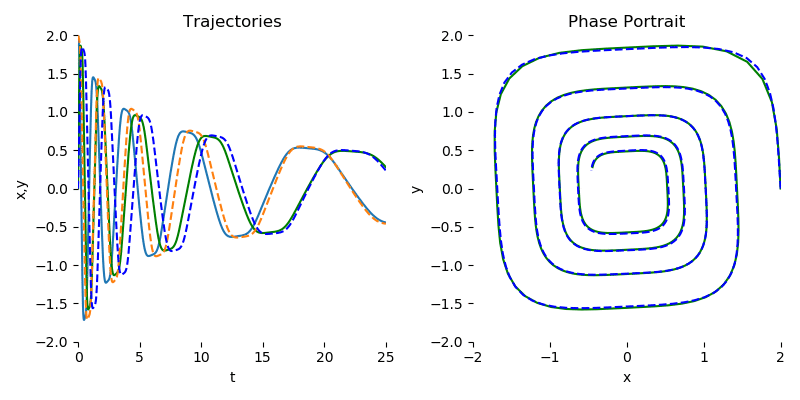
左图是这个螺旋曲线的动点在不同时刻$t$下在$x$轴和$y$的坐标变化序列,虚线是预测序列,实线是目标序列。右图是这个螺旋曲线经过所有时间后,在2D的$x-y$坐标系下运动的轨迹,虚线是预测轨迹,实线是目标轨迹。
图片来自torchdiffeq官方github仓库[1]
而且,如果目标方程确定的话,实际上就让网络拟合这一个方程就可以了,不需要任何的额外输入(除了初始状态$(x_0, y_0)^\top$),所以也就不需要像Neural ODE[2]或者Latent ODE[3]原文里的RNN、ODE-RNN作为编码器(文章里面经常称为Recognition Model,应该是领域术语),生成隐状态服从的高斯分布$z(t_0) \sim \mathcal{N}(\mu, \sigma)$的均值和方差。
$$
\begin{equation}
z(t+\epsilon) = z(t) + \int_{t}^{t+\epsilon} f(z(t’), t’, \theta)dt’
\end{equation}
$$
有趣的是,Neural ODE为了和ODE保持一致,像上面的式子一样,能够不断地在同一个微分函数上积分,然后与初值相加,确实是不允许输入和输出的$z$形状不一致的(容易联想到Diffusion扩散模型的基本原理和ODE有联系,这就是另一些故事了,感兴趣可以去搜相应的工作)。也就是说,不允许$z(t_0)$是一个隐式的特征,而剩下的$z(t>t_0)$是显式的预测值。所以,凡是使用了隐式特征的Neural ODE,都需要一个额外的解码器,可以参见这个示例代码。
所以,从某种意义上来说,前面几篇笔记反复提到的“错误”也不全错,对复杂过程的建模,而且需要一个编码器生成初始状态作为条件condition,就是需要在隐式特征的状态上做积分。但是,如果解码器$\phi$是线性的且没有偏置,那么输出仍然服从和隐式状态一样的变化量关系约束。由于对任意$t$都有$y(t)=\phi(z(t))$:
$$
\begin{align}
& y(t+\epsilon) = \phi(z(t+\epsilon)) \nonumber \\
& = \phi\left(z(t) + \int_{t}^{t+\epsilon} f(z(t’), t’, \theta)dt’\right) \nonumber \\
& = \phi(z(t)) + \phi\left(\int_{t}^{t+\epsilon} f(z(t’), t’, \theta)dt’\right) \nonumber \\
& = y(t) + \Delta y|_t^{t+\epsilon} \\
\end{align}
$$
其中,最后这项$\phi(\cdot)$可以记作$\Delta y|_t^{t+\epsilon}$,也就是$\epsilon$长度时间内$y$的变化量。不妨令$\epsilon \rightarrow 0$,则$\epsilon = dt$,可以推出:
$$
\begin{align}
& y(t+\epsilon) - y(t) = \Delta y|_t^{t+\epsilon} \nonumber \\
& \Rightarrow \lim_{\epsilon \rightarrow 0} \frac{y(t+\epsilon) - y(t)}{\epsilon} = \lim_{\epsilon \rightarrow 0} \frac{\Delta y|_t^{t+\epsilon}}{\epsilon} \nonumber \\
& \Rightarrow \frac{dy}{dt} = \lim_{\epsilon \rightarrow 0} \frac{\Delta y|_t^{t+\epsilon}}{\epsilon} \nonumber \\
& \Rightarrow \int_t^{t+\epsilon} \frac{dy}{dt} dt = \int_t^{t+\epsilon} \lim_{\epsilon \rightarrow 0} \frac{\Delta y|_t^{t+\epsilon}}{\epsilon} dt \nonumber \\
& \Rightarrow \int_t^{t+\epsilon} \frac{dy}{dt} dt = \Delta y|_t^{t+\epsilon} \nonumber\\
& \Rightarrow y(t+\epsilon) = y(t) + \int_t^{t+\epsilon} \frac{dy}{dt} dt \nonumber \\
\end{align}
$$
为什么非线性的解码器不能做到这点呢?最简单的例子就是指数函数:$e^{(a+b)} = e^a \cdot e^b \neq e^a + e^b$,$a$和$b$相加后再输入的结果,不能等于$a$和$b$分别输入再相加的结果。比较遗憾的是,Neural ODE的默认解码器是非线性的,所以甚至不能满足式子(2)的关系。所以,将隐式特征线性解码成显式状态(例如上图例子中的$(x, y)^\top$),对应的显式状态仍然满足和式子(1)一样的积分关系。只是$\frac{dy}{dt}$无法用一个函数$f$来表示,而是像上面的第二步推导是一个极限。
随机微分方程 Stochastic Differential Equation
如果有观察过Neural ODE[2]和Latent ODE[3]原文的实验部分,可以发现它们的拟合的时间序列往往是平滑形式的。但是,很多真实的物理过程是存在大量随机的,例如流体运动、热量传递等,底层都是分子原子的布朗运动(Brownian Motion)。只要输入相同,微分方程$f(\cdot)$输出一般没有随机性。当然,其基于VAE的思想确实能够通过对若干次初始状态$z(t_0) \sim \mathcal{N}(\mu, \sigma)$的采样,最后对预测结果算均值来一定程度上缓解这个问题,但是最终的曲线趋势仍然是平滑的。
以下推导直接参考剑桥大学2019年出版的教材“Applied Stochastic Differential Equations”[5](Kevin Course和Prasanth B. Nair在2023年发表的Nature正刊[6]和NeurIPS正会[7]论文就参考了这个教材)。
为了描述一个带有噪声过程$w(t)$的隐式状态$x(t)$变化过程,我们将常微分方程$\frac{dx(t)}{dt} = f(x(t), t)$改写为:
$$
\begin{equation}
\frac{dx(t)}{dt} = f(x(t), t) + L(x(t), t)w(t)
\end{equation}
$$
其中,随机过程$w(t)$本身与状态$x(t)$无关,一般是白噪声过程(White Noise),例如外界随机影响、内部随机运动。而$L(x(t), t)$和$f$一样,是一个与$x(t)$有关的任意函数(也可以与$x(t)$无关,带$x(t)$的项目就为0)。
那么,和之前的笔记一样,给定初值$x(t_0)$,对随机微分方程式子(3)求积分得到任意$t$时刻下的$x(t)$:
$$
\begin{align}
& x(t) - x(t_0) \nonumber \\
& = \int_{t_0}^{t} f(x(t), t) dt + \int_{t_0}^{t} L(x(t), t)w(t) dt \\
\end{align}
$$
显然,由于第一个积分是确定性的,无论是求解析解还是数值解,都是可行的方案。问题比较大的是第二个积分,因为它带有一个随机过程$w(t)$.。将这个积分写成极限形式:
$$
\begin{align}
& \int_{t_0}^{t} L(x(t), t)w(t) dt \nonumber \\
& = \lim_{n \rightarrow \infty} \sum_k L(x(t^*_k), t^*_k)w(t^*_k)(t_{k+1} - t_k), \nonumber \\
& \mathrm{where} \nonumber \\
& t_0 < t_1 < \cdots < t_n = t, ~~ t^*_k \in [t_k, t_{k+1}]
\end{align}
$$
简而言之,将$[t_0, t]$划成$n \rightarrow \infty$个小区间,在任意两个区间之间计算矩形面积,宽为$t_{k+1} - t_{k}$,高为这个区间中取一个点$t^*_k$对应的函数值$L(x(t^*_k), t^*_k)w(t^*_k)$,将所有矩形面积相加即为积分。然而,由于随机过程$w(t^*_k)$并没有上下界,所以这样取一个或多个$t^*_k \in [t_k, t_{k+1}]$代表小区间矩形高度是没有意义的(形象一点就是一会儿很高、一会儿很低)。
为了保证这个代表小区间高度的被积函数是有界的,我们需要尝试将白噪声过程$w(t)$替换为有界的随机过程。布朗运动(Brownian Motion)就比较合适,$w(t)dt = d\beta(t) \sim \mathcal{N}(0, Qdt)$,$Q$为方差的扩散系数,满足以下的性质:
- 给定时间区间$\Delta t_k = t_{k+1} - t_k$,$\Delta \beta_k = \beta(t_{k+1}) - \beta(t_k) \sim \mathcal{N}(0, Q\Delta t_k)$都是一个有界的高斯分布。
- 初始时间的$\beta(t_0)=0$,且在不重叠的时间段,$\Delta \beta_k$的值是相互独立的,不会被前后的差值影响。
由此,我们可以代入$w(t)dt = d\beta(t)$,重写式子(5)为:
$$
\begin{align}
& \int_{t_0}^{t} L(x(t), t)d\beta(t) \nonumber \\
& = \lim_{n \rightarrow \infty} \sum_k L(x(t^*_k), t^*_k)(\beta(t_{k+1}) - \beta(t_k)), \nonumber \\
& \mathrm{where} \nonumber \\
& t_0 < t_1 < \cdots < t_n = t, ~~ t^*_k \in [t_k, t_{k+1}] \nonumber \\
\end{align}
$$
但是,在区间中取不同的点$t^*_k \in [t_k, t_{k+1}]$,对于函数$L(x(t^*_k), t^*_k)$取值也有影响,最终影响积分值。因此,在这里直接采用伊藤随机积分(Itô Stochastic Integral),取$t=t_k$,保证最终的积分值是唯一的。
$$
\begin{align}
& \int_{t_0}^{t} L(x(t), t)d\beta(t) \nonumber \\
& = \lim_{n \rightarrow \infty} \sum_k L(x(t_k), t_k)(\beta(t_{k+1}) - \beta(t_k)), \nonumber \\
& \mathrm{where} ~ t_0 < t_1 < \cdots < t_n = t
\end{align}
$$
最终,式子(4)可以重写为:
$$
\begin{align}
& x(t) - x(t_0) \nonumber \\
& = \int_{t_0}^{t} f(x(t), t) dt + \int_{t_0}^{t} L(x(t), t)d\beta(t) \nonumber \\
\end{align}
$$
相应的随机微分方程,被称为伊藤随机微分方程(Itô SDE):
$$
\begin{align}
& \frac{dx(t)}{dt} = f(x(t), t) + L(x(t), t)\frac{d\beta(t)}{dt} \nonumber \\
& \Rightarrow dx(t) = f(x(t), t)dt + L(x(t), t)d\beta(t)
\end{align}
$$
其中,函数$f(\cdot)$被称为漂移函数(Drift Function),因为它决定了整个变化过程的总体趋势。函数$L(\cdot)$被成为扩散函数(Diffusion Function),因为它基于布朗运动,决定了随机运动(类似于粒子扩散)的幅度。
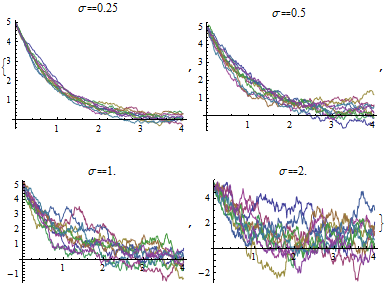
高斯过程近似 Gaussian Process Approximation of SDE Solutions
在Kevin Course和Prasanth B. Nair的两篇论文[6][7]中,都提到了可以通过高斯过程(Gaussian Process)来近似解随机微分方程。首先,包括这两篇论文,以及剑桥大学教材[5],都将任务场景描述为了以下的“连续-离散”系统(Continuous-Discrete System),意思是观测值$y(k)$是离散的、不随时间连续的,而系统的状态$x(t)$是在时间上连续、且带有随机性质的。根据式子(7),引入观测值与内在状态的关系:
$$
\begin{align}
& dx(t) = f(x(t), t)dt + L(x(t), t)d\beta(t), \nonumber \\
& y(k) = h(x(t_k)) + r_k
\end{align}
$$
其中$r_k \sim \mathcal{N}(0, R)$为观测时的底噪,$h$是状态$x(t_k)$到观测$y(k)$的映射函数。实际上,这就是状态估计的基本任务设置。这里省略一个证明,就是线性随机微分方程(漂移函数$f$是线性的)的解$x(t)$是一个高斯过程。对应线性SDE写作:
$$
\begin{align}
d\tilde{x}
& = \tilde{f}(x(t), t)dt + L(t)d\beta(t), \nonumber \\
& = [-A(t)\tilde{x}(t)+b(t)]dt + L(t)d\beta(t) \\
\end{align}
$$
其中,线性参数$A(t)$和$b(t)$是待求解项。为了简化书写,省略式子(9)扩散函数$L$中的$x(t)$。根据教材[5],这个解的边际分布(Marginal Distribution,只包含一部分变量的分布,例如2D高斯分布在其中一个1D轴上的投影是1D高斯分布)是$q(x(t))=\mathcal{N}(x(t)|m(t), P(t))$,其中$m(t)$和$P(t)$分别是$x(t)$的期望和标准差,且应当服从如下的微分方程约束(教材原文是矩阵形式的):
$$
\begin{align}
& \frac{d\mathbf{m}(t)}{dt} = -\mathbf{A}(t)\mathbf{m}(t) + \mathbf{b}(t) \\
& \frac{d\mathbf{P}(t)}{dt} = -\mathbf{A}(t)\mathbf{P}(t) - \mathbf{P}(t)^\top\mathbf{A}(t) + \mathbf{L}(t)\mathbf{Q}\mathbf{L}(t)^\top
\end{align}
$$
由于不是重点,这里简要介绍之后的步骤。在理想情况下,边际分布$q(x(t))$应当与对应的真实分布$p(x(t)|y(t))$一致,也就是计算KL散度$\mathrm{KL}(q || p)$。使用拉格朗日乘子法(Lagrange Multipler Function),最小化KL散度公式,并使用两个拉格朗日乘子$\mathbf{\lambda}(t)$、$\mathbf{\Psi}(t)$联立约束等式(10)和(11),求解后得到待求解的线性参数$A(t)$和$b(t)$表达式:
$$
\begin{align}
& \mathbf{A}(t) = -\mathbb{E}_q[f(\mathbf{x}(t), t)] + 2\mathbf{L}(t)\mathbf{Q}\mathbf{L}^\top(t)\mathbf{\Psi}(t) \nonumber \\
& \mathbf{b}(t) = \mathbb{E}_q[f(\mathbf{x}(t), t)] + \mathbf{A}(t)\mathbf{m}(t) + \mathbf{L}(t)\mathbf{Q}\mathbf{L}^\top(t)\mathbf{\lambda}(t) \nonumber \\
\end{align}
$$
具体过程参见教材[5]的第12.8章节。总而言之,通过假定(其实就是近似)SDE中的未知漂移函数$f(\cdot)$为线性、同时根据线性SDE的解$x(t)$是高斯过程的性质,得到其边际分布$q(x(t))$均值方差的约束式子(10)和(11),联立边际分布和真实分布的KL散度以及这些约束式子,用拉格朗日乘子法计算出$A(t)$和$b(t)$,代入式子(9)得到近似真实SDE的线性SDE。
在状态估计中的应用 Application in State Estimation
这里以Kevin Course和Prasanth B. Nair的2023年Nature论文[6]为例。首先,他们分别定义了观测值$y(t)$和隐式状态$x(t)$的映射函数、以及先验和后验两个SDE:
$$
\begin{align}
& y(t) = h(x(t)) + r(t) \\
& dx(t) = f_\theta(x(t), t)dt + \Sigma_\theta(t)d\beta(t) \\
& dx(t) = [-A_\phi(t)x(t)+b_\phi(t)]dt + \Sigma_\theta(t)d\beta(t) \\
\end{align}
$$
其中,式子(13)是先验SDE,也就是我们待求的SDE;式子(14)是后验SDE,就是通过上一章节的高斯过程近似方法,得到的具体$A_\phi(t)$和$b_\phi(t)$。可以认为,后验SDE是一个用线性SDE近似得来的额外参考,相比直接让一个黑盒的Neural SDE[4]用参数$\theta$去拟合数据,更加地符合SDE的基本规律(也就是说,至少不能比线性SDE的结果还差)。
由此,文章提出的学习目标ELBO(证据下界,Evidence Lower Bound)是:
$$
\begin{equation}
\begin{split}
& \log p(\mathcal{D}) \\
& = \log \mathbb{E}_{p(\theta)}\left[\mathbb{E}_{\tilde{P}|\theta}\left[\prod_{i=1}^\mathrm{N} p(y(t_i) | x(t_i))\right]\right] \\
&\geq \sum_{i=1}^{N} \mathbb{E}_{p_\phi(x(t_i))}[\log p(y(t_i) | x(t_i))] \\
&-\frac{1}{2}\int_{0}^{T} \mathbb{E}_{q_\phi(x(t))q_\phi(\theta)}{\lvert\lvert{r(x(t), \theta,\phi)}\rvert\rvert_{\Sigma_\theta Q\Sigma^\top_\theta}^2}
\,dt \\
& - D_{KL}(q_\phi(\theta) \mid \mid p(\theta)) = \mathrm{ELBO}(\phi)
\end{split}
\end{equation}
$$
其中,$\mathbb{E}_{\tilde{P}|\theta}$是待求的先验SDE式子(13)对应的期望,$\mathbb{E}_{p(\theta)}$是参数$\theta$所在空间的概率分布对应的期望(实际上这个期望可以拿掉,因为无法对参数空间采样,或者说近似为当前学到的参数$\theta$,毕竟当前参数既然出现了,概率肯定最大)。 $r(x(t)\theta,\phi) = -A_\phi(t)x(t) + b_\phi(t) - f_\theta(x(t), t)$,也就是近似后验SDE约束待求先验SDE,而且只有漂移函数项约束。同时也用到了后面的扩散函数项$\Sigma_\theta$,也就是$\lvert\lvert{v}\rvert\rvert_{\Sigma_\theta Q\Sigma^\top_\theta}^2=v^\top(\Sigma_\theta Q\Sigma^\top_\theta)^{-1}v$。最后一项是对参数分布的约束,$p(\phi)$为给定的先验约束(一般是高斯分布),$q_\phi(\theta)$为真实的参数分布。
实际上,在式子(15)的不等式中,只有不等号右边的第一、二项是真的下界,用到了琴生不等式(Jensen’s Inequation),$\mathbb{E}[-\log(p)] \geq -\log\mathbb{E}(p)$,应该是参考了陈天琦团队的2020年AISTATS会议论文“Scalable gradients for stochastic differential equations”[8],他们也定义了先验、近似后验两个SDE,然后对ELBO式子做了分解,得到了一个重构真实值项和一个近似后验SDE约束先验SDE的积分项,也就是第一、二项。
所以,在式子(15)中,KL散度是后来加上的,所以和之前的变分推断笔记有一定的区别,那边的KL散度是推导出来的,用来约束隐式特征,但是这边的KL散度是约束的参数。只是形式类似,都是重构真实值和KL散度约束的组合。
重参数技巧和均摊分析 Reparameterization and Amortization
与之前的变分推断笔记类似,也是为了避免多次前向,那边是给中间的隐式特征分布从$\mathcal{N}(\mu, \sigma)$转为$\mathcal{N}(0, I)$,这里是对隐式特征分布$q_\phi(x(t))$。因为,这是近似后验SDE(参数为$\phi$)输出的当前时刻$t$的隐式状态$x(t)$概率分布,这个概率分布是很难精确找到的,毕竟SDE是带随机性的。当然,也可以通过反复前向多次、采多个$x(t)$的方式来近似它。
但是,可以回想第3章节“高斯过程近似”里面,为了求这个线性SDE的式子(10)和(11),我们已经推导出了$x(t)$的边际分布,也就是$q(x(t))=\mathcal{N}(x(t)|m(t), P(t))$,所以,我们可以直接用这个高斯分布,代替多次前向采样得到的$q_\phi(x(t))$。但是,就算不采样$x(t)$了,式子(15)对应的$r(\cdot)$函数里,每个时刻对应的$A_\phi(t)$和$b_\phi(t)$还是照样得算的。
此时,可以看到式子(10)和(11),刚好就是$A_\phi(t)$和$b_\phi(t)$构成的,由此可以重新整理成$A_\phi(t)$和$b_\phi(t)$的表达式,然后代入$r(\cdot)$函数。其中,$\oplus$是克罗内克加法(Kronecker Addition)。具体细节可以参见Nature原文[6]:
$$
\begin{align}
& r(x(t), t, \theta, \phi) \nonumber \\
& = \mathrm{vec}^{-1}((P_\phi(t) \oplus P_\phi(t) )^{-1}\mathrm{vec}(\Sigma_\theta Q \Sigma_\theta^\top \nonumber \\
& - \frac{dP_\phi(t)}{dt}))(m_\phi(t) - x(t)) + \frac{dm_\phi}{dt} - f_\theta(x(t), t) \\
\end{align}
$$
另外,之前的笔记里面有简要地提到均摊分析(Amortized Analysis)的概念,当时是为了强调参数量不应当与数据规模挂钩,否则数据量无限大则参数无限大,无法实际应用。Kevin Course和Prasanth B. Nair在NeurIPS 2023上发表的论文“Amortized Reparametrization: Efficient and Scalable Variational Inference for Latent SDEs”[7],在标题里面就同时提到了重参数技巧和均摊分析。在这篇文章里,重参数技巧和Nature版本论文一致,均摊分析指的是,尝试将整段长度为N的时间序列数据,切分为M份,每份长度为N/M,从而更好地实现并行化的训练和预测。
结语 Conclusions
至此,已经写好了三篇笔记,基本搞懂了Neural ODE、SDE以及状态估计。但是,还有很多的细节没有搞懂,例如这篇里面省略的若干推导过程,以及状态估计的两篇论文[6][7]的更多应用场景、数据和建模方式,尤其是NeurIPS论文的附加材料[7]给出了针对不同任务的网络结构设计。此外,现在的笔记内容全是个人理解,难免错漏,之后肯定要修改。
令人感到意外的是,三篇笔记前后关联了很多知识点,ODE和SDE的微分和积分形式、变分推断中的ELBO、重参数技巧、均摊分析。回想我在第一篇笔记里吐槽的“各种统计学、数据科学、机器学习的视频都在强调”,就体现了统计机器学习领域各理论分支的共通之处。希望这次的笔记能作为一个全新的开始,让我们继续探索,看懂更多精彩的东西!
参考资料
- [1] Chen R T Q. https://github.com/rtqichen/torchdiffeq
- [2] Chen R T Q, Rubanova Y, Bettencourt J, et al. Neural ordinary differential equations[J]. Advances in neural information processing systems, 2018, 31.
- [3] Rubanova Y, Chen R T Q, Duvenaud D K. Latent ordinary differential equations for irregularly-sampled time series[J]. Advances in neural information processing systems, 2019, 32.
- [4] Tzen B, Raginsky M. Neural stochastic differential equations: Deep latent gaussian models in the diffusion limit[J]. arXiv preprint arXiv:1905.09883, 2019.
- [5] Särkkä S, Solin A. Applied stochastic differential equations[M]. Cambridge University Press, 2019.
- [6] Course K, Nair P B. State estimation of a physical system with unknown governing equations[J]. Nature, 2023, 622(7982): 261-267.
- [7] Course K, Nair P B. Amortized Reparametrization: Efficient and Scalable Variational Inference for Latent SDEs[C]//Thirty-seventh Conference on Neural Information Processing Systems. 2023.
- [8] Li X, Wong T K L, Chen R T Q, et al. Scalable gradients for stochastic differential equations[C]//International Conference on Artificial Intelligence and Statistics. PMLR, 2020: 3870-3882.
感谢阅读!如有意见和建议,欢迎通过首页的联系方式联系作者。
本文参考资料均来源于网络,作者保留相关权利,转载请注明出处。