Notes About Deep Q-Learning

A reinforcement process is one in which some aspects of the behavior of
a system are caused to become more (or less) prominent in the future
as a consequence of the application of a “reinforcement operator”.
in Steps Toward Artificial Intelligence, Marvin Minsky

本文是关于深度Q强化学习Deep Q-Learning的学习笔记
主要包括前置知识、策略梯度PG、近端策略优化PPO、深度Q网络DQN、深度确定性策略梯度DDPG和相关扩展知识

前言 Introduction

作为著名的人工智能“达特茅斯会议”主要发起人、1969年图灵奖获得者，马尔文·明斯基在1961年发表了论文《迈向人工智能》，并首次定义了强化学习Reinforcement Learning的基本概念：“通过应用强化操作，使得系统行为的某些方面在未来更加（或更不）显著，这一过程叫做强化过程”。这里的“强化操作”，指的是系统与环境交互、获得奖励反馈并学习之后，这个系统的行为在未来交互中，发生了向着潜在奖励更高方向的、定向的变化，也即“强化”。

基于操作强化（Operant Reinforcement）的学习系统，图片来自《迈向人工智能》论文原文^[1]

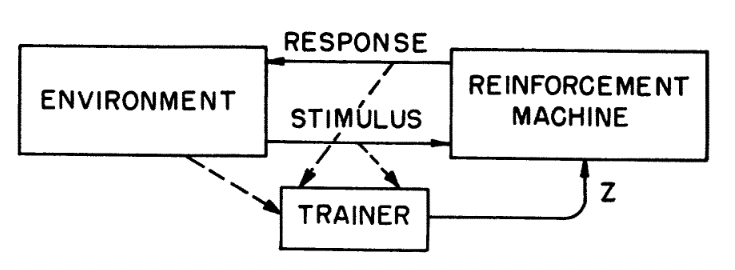
结合论文原图，可以看到从1961年至今，强化学习的基本框架是万变不离其宗的。在很长一段时间里，强化学习往往被诟病其应用范围过窄，除了游戏、博弈等仿真成本较低的领域，更复杂的自动驾驶、工业控制等领域仍然是非强化学习为主的。随着OpenAI提出了全新的大语言模型方案，人类反馈的强化学习RLHF（Reinforcement Learning from Human-Feedback）以及其背后的近端策略优化PPO（Proximal Policy Optimization）将强化学习带到了聚光灯下。更进一步地，OpenAI在各种场合暗示了下一代模型Q*，同样是基于深度Q强化学习的搜索采样。

需要强调的是，强化学习已经有若干优质教程在前，包括李宏毅老师的《深度强化学习》系列课程^[2]、Sutton教程英文实体书^[3]、以及EasyRL教程中文实体书+在线教程“蘑菇书”^[4]。本文参考了前述教程，仅摘录个人认为需要重点学习的内容，并加入了若干个人理解。如需更深入地学习，请优先参考前述更加系统完备的课程和书籍。

预备知识 Preliminaries

从提出这一任务开始，强化学习的关键要素就是与环境Environment的交互。交互过程中，强化学习模型（也叫智能体Agent）本身可以是黑箱，但仍然需要这3个重要组成部分：

1. 策略Policy：根据当前状态State，决定应该采取哪些行为Action；
2. 奖励Reward：根据当前状态State，决定采取特定的行为Action，环境反馈给模型的奖励（还有新的状态）；
3. 价值函数Value Function：基于采取行为后将获得的奖励Reward，衡量当前状态State好坏（是否需要改变）。

策略 Policy

首先，策略可以分为两种，随机性策略和确定性策略。随机性策略Stochastic Policy，是按照特定概率$p$选择采取某一种行动$a^*$，这种选择的行为可以定义为一个$\pi$函数，可以写成在一个概率分布$p$中采样的形式：

$$
\begin{equation}
a^* \sim \pi(a|s) = p(a_t=a|s_t=s)
\label{sto-policy}
\end{equation}
$$

例如，有2种状态，随机选择到的概率分别为$p$和$1-p$。确定性策略Deterministic Policy，则是直接采取最有可能的动作，所以可以直接写作在状态s的情况下的一种查表操作$\pi(s)$：

$$
\begin{equation}
a^* = \pi(s) = \arg\max_a \pi(a|s)
\label{det-policy}
\end{equation}
$$

虽然很多教程都在强调，引入随机性能够通过多次采样$a^* \sim \pi$，从而采取多样化的行动，更好地探索环境。但是，环境并不总是可以完美仿真的。在一些真实环境下，多次采样是有代价的。

集束搜索Beam Search，是自回归文本生成（Image Captioning、大语言模型问答等）常用的一种采样方法
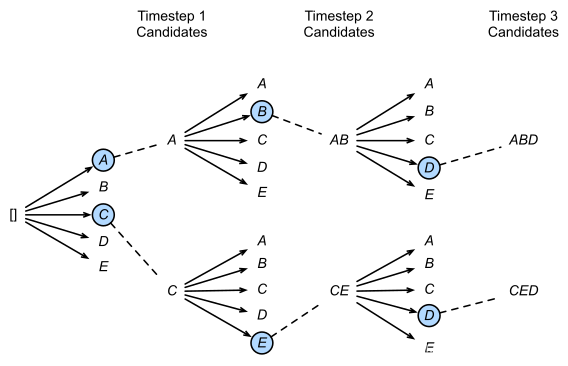
相比使用Top-1的贪婪方法，更容易找到全局最优

类比集束搜索Beam Search，即使是在成本较低的仿真环境中，如果行为本身是高维度的（例如有很多关节的机器人），在每一步采样后，会分叉出庞大的行为轨迹树，采样成本也是巨大的；在采样之后，也需要对每条采样到的行为轨迹，计算相应的奖励，这个计算开销同样是巨大的。因此，确定性策略反而具有了样本需求小的优势。

奖励 Reward

在状态$s$下，当智能体Agent做出了行为$a$，则相应的能够从环境得到反馈的奖励$R(s, a)$。为了兼容随机性策略的“在概率分布中多次采样”的情况，将$R(s, a)$写成条件期望的形式，也就是给定概率密度函数$g(r_{t+1} | s_t=s, a_t=a)$的积分：

$$
\begin{equation}
R(s, a) = \mathbb{E}[r_{t+1} | s_t=s, a_t=a] = \int_{R_{t+1}} r \cdot g(r_{t+1} | s_t=s, a_t=a) dr
\end{equation}
$$

其中，$R_{t+1}$是此时所有可能的奖励，可以看做所有可能奖励构成的空间，在该空间按概率$g$积分，就是多次采样后的总体奖励。但是，如果只考虑眼前的奖励$R(s, a)$，容易陷入贪婪方法的局部最优。因此，即使只采取了当下的行为$a$，也必须长远考虑从$t+1$到$t+\infty$的奖励，从而尽可能逼近全局最优，也就是价值函数Value Function。

价值函数 Value Function

虽然确实需要考虑从$t+1$到$t+\infty$的奖励，但最好能够用尽可能短的时间，获得尽可能多的奖励。因此，对于时间段$k \in (0, \infty)$，设置一个折扣因子$\gamma^k$（Discount Factor），在更近的时间值更大，反之则更小。

价值函数也分为两种：V函数和Q函数。V函数就是简单的折扣因子$\gamma^k$乘以未来奖励$r_{t+k+1}$。还是因为随机性策略需要“在概率分布中多次采样”，对于当前状态$s$下的策略$\pi$（所以有一个下标，并不是对$\pi$求期望），需要计算条件期望：

$$
\begin{equation}
V_\pi(s) = \mathbb{E}_\pi[G_t | s_t = s] = \mathbb{E}_\pi\left[ \sum_{k=0}^{\infty} \gamma^k r_{t+k+1} | s_t = s\right]
\label{v-function}
\end{equation}
$$

Q函数额外引入了动作变量$a$，从而能够在后续的深度Q学习中，通过Q函数得到进入某个状态需要采取的最优动作。

$$
\begin{equation}
Q_\pi(s, a) = \mathbb{E}_\pi[G_t | s_t = s, a_t = a] = \mathbb{E}_\pi\left[ \sum_{k=0}^{\infty} \gamma^k r_{t+k+1} | s_t = s, a_t = a\right]
\label{q-function}
\end{equation}
$$

那么，为什么要用价值函数Q函数得到最优动作$a^*$，而不是直接像式子$\eqref{sto-policy}$和$\eqref{det-policy}$，通过策略$\pi(\cdot)$得到呢？这就涉及到强化学习中对于智能体类型的划分问题：“基于价值的智能体”和“基于策略的智能体”。

智能体的类型 Variants of Agents

在EasyRL“蘑菇书”中，已经详细介绍了“基于价值的智能体”和“基于策略的智能体”，这里简要地概括一下：

• 基于价值的智能体：显式地学习价值函数，隐式地学习策略，策略是从价值函数中推算出来的（价值表格查表、价值函数建模）。例如，深度Q学习Deep Q-Leanring需要显式学习一个Q模型作为黑盒的价值函数。
• 基于策略的智能体：显式地学习策略，无需价值函数，策略就是智能体输出的动作。例如，策略梯度Policy Gradient就是通过基于损失函数来直接指导模型的策略，同时能够处理连续型、离散型动作策略的问题。
• 同时基于策略和价值的智能体：演员-评论员方法Actor-Critic结合了前述两种方法，根据智能体Actor的动作，价值函数Critic给出相应的价值。由于价值是未来奖励构成的，定向的价值可以加快基于策略方法的探索学习速度。

同时，另一种常见的分类“有模型强化学习智能体”和“无模型强化学习智能体”，也可以总结如下：

• 有模型强化学习智能体：在智能体内部，需要对与之交互的真实环境进行显式的建模，构建一个包括状态转移函数$p(s_{t+1}|s_t, a_t)$以及奖励函数$R(s_t, a_t)$的虚拟环境，从而在执行动作$a_t$前，对下一步对的状态和奖励进行预测。

• 无模型强化学习智能体：无需对交互的环境进行建模，取而代之的是需要大量的采样来估计状态、动作和奖励函数，比有模型方法需要更多的数据。相比带有偏差的、容易过拟合的虚拟环境，无模型方法的泛化能力更强。

李宏毅老师教程视频截图，图片来自shaoeChen的笔记

此外，还需要强调一种基于策略学习机制的分类方式：同策略“On-Policy”和异策略“Off-Policy”，具体如下：

• 同策略On-Policy：学习策略的智能体和与环境互动的智能体是同一个智能体，类似于自己亲自玩游戏。
• 异策略Off-Policy：学习策略的智能体和与环境互动的智能体是不同的智能体，类似于看别人在玩游戏。

同策略方法的缺点在于，基于策略的智能体在更新参数$\theta’ = \theta + \eta \nabla R_\theta$之后，隐式编码在模型参数中的策略$\pi_\theta$就变成了$\pi_{\theta’}$，基于原有策略采样出的行为轨迹$\tau \sim p_\theta(\tau)$，就无法重复用在对奖励函数的梯度计算上，需要在环境中用$\pi_{\theta’}$重新采样出新的轨迹$\tau’ \sim p_{\theta’}(\tau’)$，才能计算新的$\nabla R_{\theta’}$。

与之不同的是，异策略方法能够避开反复采样的低效过程，用一个固定的额外模型与环境交互得到一批数据，用这批数据反复训练当前模型，从而避开了反复采样的过程。从这个思路出发，是对策略梯度PG的若干改进，包括重要性采样、近端策略优化PPO等。但首先需要了解为什么$\nabla R_\theta$需要反复采样。

策略梯度 Policy Gradient

前面描述的奖励函数$R_\theta$，实际上是当前模型$\theta$经历了各种轨迹$\tau$的总体奖励，可以认为是不同轨迹奖励$R(\tau)$的期望：

$$
\begin{equation}
R_\theta = \sum_\tau p_\theta(\tau)R(\tau) = \mathbb{E}_{\tau \sim p_\theta(\tau)}[R(\tau)]
\label{reward-expect}
\end{equation}
$$

注意这里期望的下标表示的是轨迹$\tau$服从了概率分布$p_\theta(\tau)$，也就是有$p$这么大的概率能采样得到$\tau$。如果参数$\theta$更新了，这个分布就改变了。那么这个分布是如何计算出来的呢？一条轨迹，包括了环境的状态改变$s$和智能体的动作$a$：

$$
\begin{equation}
\tau = \{ s_1, a_1, s_2, a_2, s_3, \cdots , a_{t-1}, s_t \}
\end{equation}
$$

除了初始状态$s_1$外，其他$a$和$s$相互关联（例如$a_1$导致了$s_2$，$s_2$又导致了$a_2$），可以得到$p_\theta(\tau)$的条件概率的连乘形式：

$$
\begin{equation}
\begin{split}
p_\theta(\tau) & = p(s_1) p_\theta(a_1|s_1) p(s_2|a_1) \cdots p(a_{t-1} | s_{t-1}) p(s_t | a_{t-1}) \\
& = p(s_1) \prod_{t} p_\theta(a_{t-1}|s_{t-1}) p(s_t|a_{t-1})
\end{split}
\end{equation}
$$

对于式子$\eqref{reward-expect}$表示的总奖励，我们希望它尽可能的大。不同于普通的损失函数通过梯度下降，优化到尽可能小，该式子应当通过梯度上升Gradient Ascent，优化到尽可能大。所以不能采用负梯度方向$-\nabla$，而是正梯度方向：

$$
\begin{equation}
\nabla R_\theta = \sum_\tau R(\tau) \nabla p_\theta(\tau) = \sum_\tau R(\tau) \nabla \left[p(s_1) \prod_{t} p_\theta(a_{t-1}|s_{t-1}) p(s_t|a_{t-1})\right]
\label{prod-p}
\end{equation}
$$

其中，总奖励$R(\tau)$是一个标量，所以不用求梯度，且允许相应的奖励函数不可微。但问题是，对乘法求导/求梯度是很难算的（$(f \cdot g)’ = f’ \cdot g + f \cdot g’$），尤其是式子$\eqref{prod-p}$还有一个连乘$\prod$，需要将乘法转换为加法。注意到$\nabla \log p = \frac{\nabla p}{p}$：

$$
\begin{equation}
\begin{split}
\nabla R_\theta & = \sum_\tau R(\tau) \nabla p_\theta(\tau) \\
& = \sum_\tau R(\tau) p_\theta(\tau) \nabla \log p_\theta(\tau) \\
& = \mathbb{E}_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla \log p_\theta(\tau)] \\
& = \mathbb{E}_{\tau \sim p_\theta(\tau)} \left[R(\tau) \nabla \left( \log p(s_1) + \sum_{t} \log p_\theta(a_{t-1}|s_{t-1}) + \sum_{t} \log p(s_t|a_{t-1}) \right) \right] \\
& = \mathbb{E}_{\tau \sim p_\theta(\tau)} \left[R(\tau) \nabla \sum_{t} \log p_\theta(a_{t-1}|s_{t-1})\right] \\
& = \mathbb{E}_{\tau \sim p_\theta(\tau)} \left[\sum_{t} R(\tau) \nabla \log p_\theta(a_{t-1}|s_{t-1})\right]
\end{split}
\label{gradient-expect}
\end{equation}
$$

其中，梯度实际上是对参数求偏导$\nabla = \frac{\partial}{\partial \theta}$，由于$p(s_1)$和$p(s_t|a_{t-1})$都是环境自身的状态变化，与智能体$\theta$无关，因此对应梯度项均为0。在实际应用中，很难通过巨量的采样得到一个准确的分布$p_\theta(\tau)$，从而准确计算式子$\eqref{gradient-expect}$的期望$\mathbb{E}_{\tau \sim p_\theta(\tau)}$。因此，假设各个轨迹的出现概率相同均为$\frac{1}{N_\tau}$，通过求均值来近似计算期望（方便起见将$t-1$改写回$t$）：

$$
\begin{equation}
\nabla R_\theta \approx \frac{1}{N_\tau} \sum_\tau \left[\sum_t R(\tau) \nabla \log p_\theta(a_{t}|s_{t})\right]
\label{pg-approx}
\end{equation}
$$

即便如上这种近似的解法省略了$p_{\theta}(\tau)$，在更新参数$\theta’ = \theta + \eta \nabla R_\theta$之后，智能体预测的各个动作概率$p_\theta(a_t|s_t)$改变，行为轨迹$\tau \sim p_{\theta’}(\tau)$的概率分布$p_{\theta’}(\tau)$随之改变，导致了必须在新参数$\theta’$上重新采样轨迹$\tau’$，才能得到正确的奖励$R(\tau’)$。

近端策略优化 Proximal Policy Optimization

既然我们不想再从新参数$\theta’$对应的分布$p_{\theta’}(\tau)$上，重新采样轨迹$\tau’$，那么最好的办法就是复用一套固定参数$\hat{\theta}$、在对应的固定分布$q_{\hat{\theta}}(\tau)$上采样的固定轨迹。对于式子$\eqref{reward-expect}$的期望，可以改写为积分形式：

$$
\begin{equation}
\begin{split}
\nabla R_\theta & = \mathbb{E}_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla \log p_\theta(\tau)] \\
& = \int [R(\tau) \nabla \log p_\theta(\tau)] p_\theta(\tau) d\tau \\
& = \int [R(\tau) \nabla \log p_\theta(\tau)] \frac{p_\theta(\tau)}{q_{\hat{\theta}}(\tau)} q_{\hat{\theta}}(\tau) d\tau \\
& = \mathbb{E}_{\tau \sim q_{\hat{\theta}}(\tau)} \left[ \frac{p_\theta(\tau)}{q_{\hat{\theta}}(\tau)} R(\tau) \nabla \log p_\theta(\tau) \right]
\end{split}
\label{importance-sampling}
\end{equation}
$$

这样，期望的下标从$\tau \sim p_\theta(\tau)$变成了$\tau \sim q_{\hat{\theta}}(\tau)$，而$q_{\hat{\theta}}(\tau)$本身是固定的，从而轨迹$\tau$也随之变成固定的了。无论$\theta$如何变化，使用这一套用$\hat{\theta}$采集的固定轨迹，就不需要智能体$\theta$与环境进行交互（行为$a$可变，状态$s$固定），奖励$R(\tau)$也一样是固定的了。为了学习参数$\theta$，只需“照本宣科”地按这条轨迹给出行为概率$p_\theta(a_t|s_t)$，获得对应当前参数$\theta$行为的轨迹条件概率$p_\theta(\tau)$。那么，相比式子$\eqref{reward-expect}$，式子$\eqref{importance-sampling}$多出来的这个$\frac{p_\theta(\tau)}{q_{\hat{\theta}}(\tau)}$有什么实际含义呢？

重要性采样Importance Sampling的示意图，其中$x$在这里指的是轨迹$\tau$，$f(\tau)=R(\tau) \nabla \log p_\theta(\tau)$
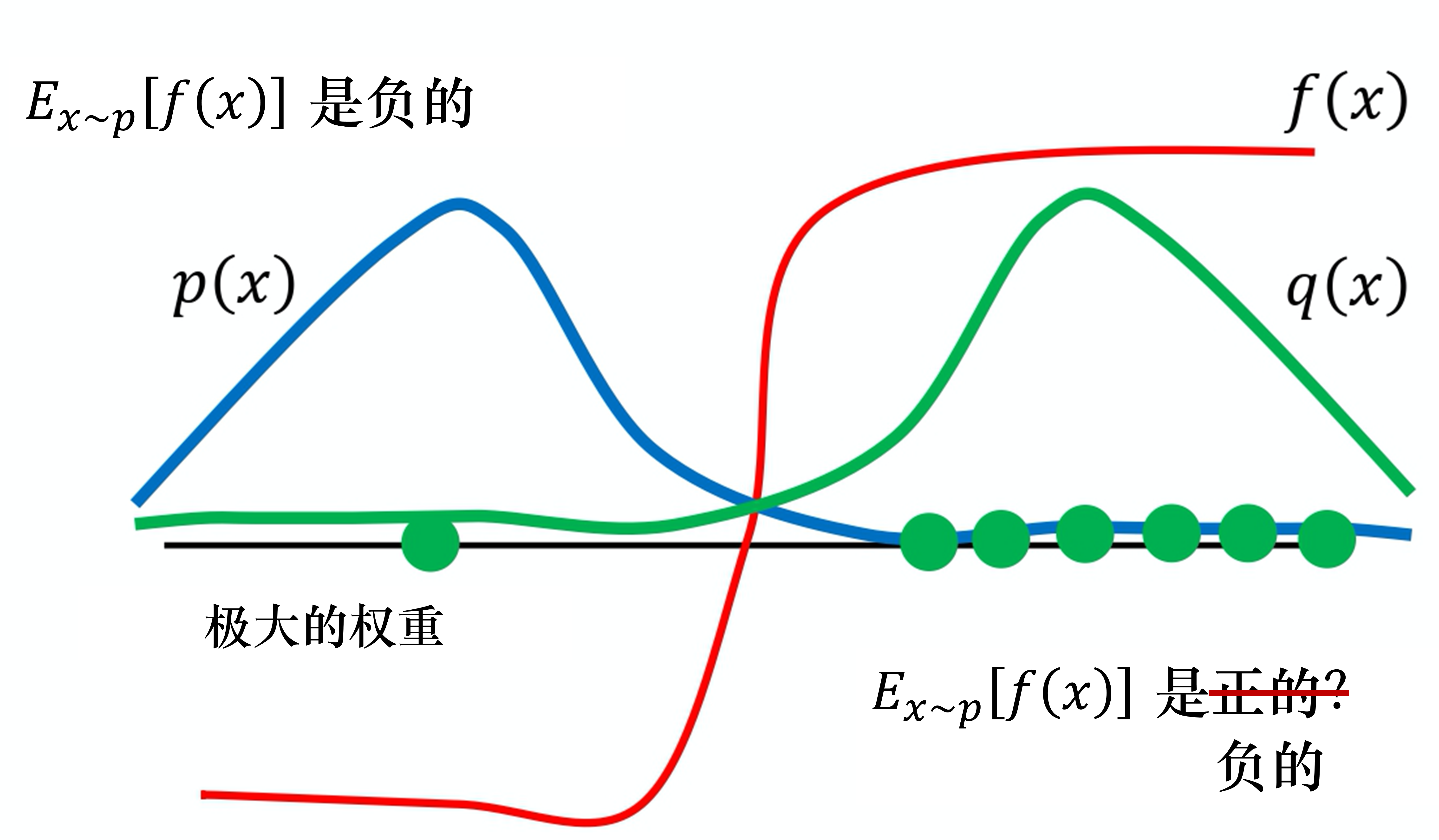
图片来自EasyRL在线版

令$f(\tau)=R(\tau) \nabla \log p_\theta(\tau)$，前面的权重$\frac{p_\theta(\tau)}{q_{\hat{\theta}}(\tau)}$叫做重要性权重。如上图所示，假设中间为原点0，$f(\tau)$的数值呈现类似Sigmoid函数的变化，也就是红线。其中，$p(\tau)$是我们想要逼近的样本概率分布，当前是大多数样本在负半轴，那么对应期望$\mathbb{E}_{\tau \sim p}[f(\tau)] < 0$。固定分布$q(\tau)$表示大多数样本在正半轴，那么采样到负半轴的概率更大。

在$q(\tau)$上，一旦采样到一个负半轴的样本，对应概率$q(\tau) \rightarrow 0$，则权重$\frac{p_\theta(\tau)}{q_{\hat{\theta}}(\tau)} \rightarrow \infty$，给对应样本的$f(\tau)$赋予了一个极大的权重，说明这个样本很接近分布$p(\tau)$，重要性很高，且此时$f(\tau) < 0$。最终，期望$\mathbb{E}_{\tau \sim q}\left[\frac{p_\theta(\tau)}{q_{\hat{\theta}}(\tau)} f(\tau)\right] < 0$，$\mathbb{E}_{\tau \sim q}\left[\frac{p_\theta(\tau)}{q_{\hat{\theta}}(\tau)} f(\tau)\right] \approx \mathbb{E}_{\tau \sim p}[f(\tau)]$。这个过程被称为重要性采样Importance Sampling。

在此基础上，近端策略优化Proximal Policy Optimization额外考虑了两个分布相差过大的情况，也就是上图中的$p_\theta(\tau)$和$q_{\hat{\theta}}(\tau)$两个峰离得非常远，很难碰巧在后者上采样到前者中的高频样本。因此，需要限制两个智能体参数$\theta$和$\hat{\theta}$的距离，可以通过KL散度的方式进行约束。定义最大化优化目标$\max J(\theta)$：

$$
\begin{equation}
\begin{split}
J(\theta) & = R_\theta - \beta \mathrm{KL}_\mathrm{PPO} \\
& = \mathbb{E}_{\tau \sim q_\hat{\theta}}\left[ \frac{p_\theta(\tau)}{q_{\hat{\theta}}(\tau)} R(\tau) \log p_\theta(\tau) \right] - \beta \mathrm{KL}(\theta, \hat{\theta})
\end{split}
\label{ppo}
\end{equation}
$$

由于约束了两个参数$\theta$和$\hat{\theta}$尽可能拉近，所以隐式编码在参数中的策略$\pi_\theta$和$\pi_\hat{\theta}$也相似。因此，近端策略优化PPO可以认为是同策略On-Policy的方法。从同策略的PG，到异策略的重要性采样，在PPO这又绕了回来，十分地有趣。而在这里，我们将这个固定参数$\hat{\theta}$、用于采样一套固定轨迹$\tau \sim q_\hat{\theta}(\tau)$的模型叫做演员Actor。

深度Q网络 Deep Q-Networks

正如之前的智能体分类中所说，除了基于策略的智能体之外，还有基于价值的智能体。这种方法不再显式地学习应该采取哪个动作，而是通过评价状态$s$或者动作-状态对$(s, a)$的价值，来间接地判断当前应当采取哪个动作。做出评价的方式，包括显式的价值表格、以及之前在式子$\eqref{v-function}$和$\eqref{q-function}$提到的价值函数，也称为评论家Critic。

离散划分的价值表格往往无法处理数值连续型的状态。但是，显式定义的价值函数也无法精确建模复杂的环境。因此，使用具有“万能逼近原理”的神经网络来表示价值函数（主要是Q函数），称为深度Q网络方法Deep Q-Networks。

首先，定义价值函数为式子$\eqref{v-function}$中的V函数$V_\pi(s)$，可以看到它只考虑了状态的价值。如果它是一个神经网络的话，我们应该如何训练它？EasyRL里面介绍了两种方法：蒙特卡洛方法和时序差分方法。

• 蒙特卡洛方法：在环境中采样各种轨迹$\tau$，在其中选取某个状态$s_t$，直接让网络学习回归式子$\eqref{v-function}$中的未来总收益$G(s_t)$，即$V_\pi(s_t) = G(s_t)$，其中$G(s_t)=\sum_t^{t+\mathrm{T}} r_t$, 每个时间点的奖励$r_t \in \tau = \{ s_{t+k}, a_{t+k}, r_{t+k} \}_{k\in (0, \mathrm{T})}$。

• 时序差分方法：蒙特卡洛方法的最大问题是忽略了单个状态的多解性，也就是有多条轨迹$\tau$都能经过同一个$s_t$，奖励$r_t$的方差很大。而且在求$G(s_t)$时，每个奖励$r_t$也如此，求和后的方差$\mathrm{Var}[\mathrm{T} \times r_t] = \mathrm{T}^2 \mathrm{Var}[r_t]$。但是，两个状态之间的转移是相对确定的，其奖励变化$r_t = V_\pi(s_t) - V_\pi(s_{t+1})$的方差也更小，因此可以学习回归$r_t$。

时序差分方法的示意图，注意是未来总收益，所以$V_\pi(s_t) > V_\pi(s_{t+1})$，图片来自EasyRL在线版

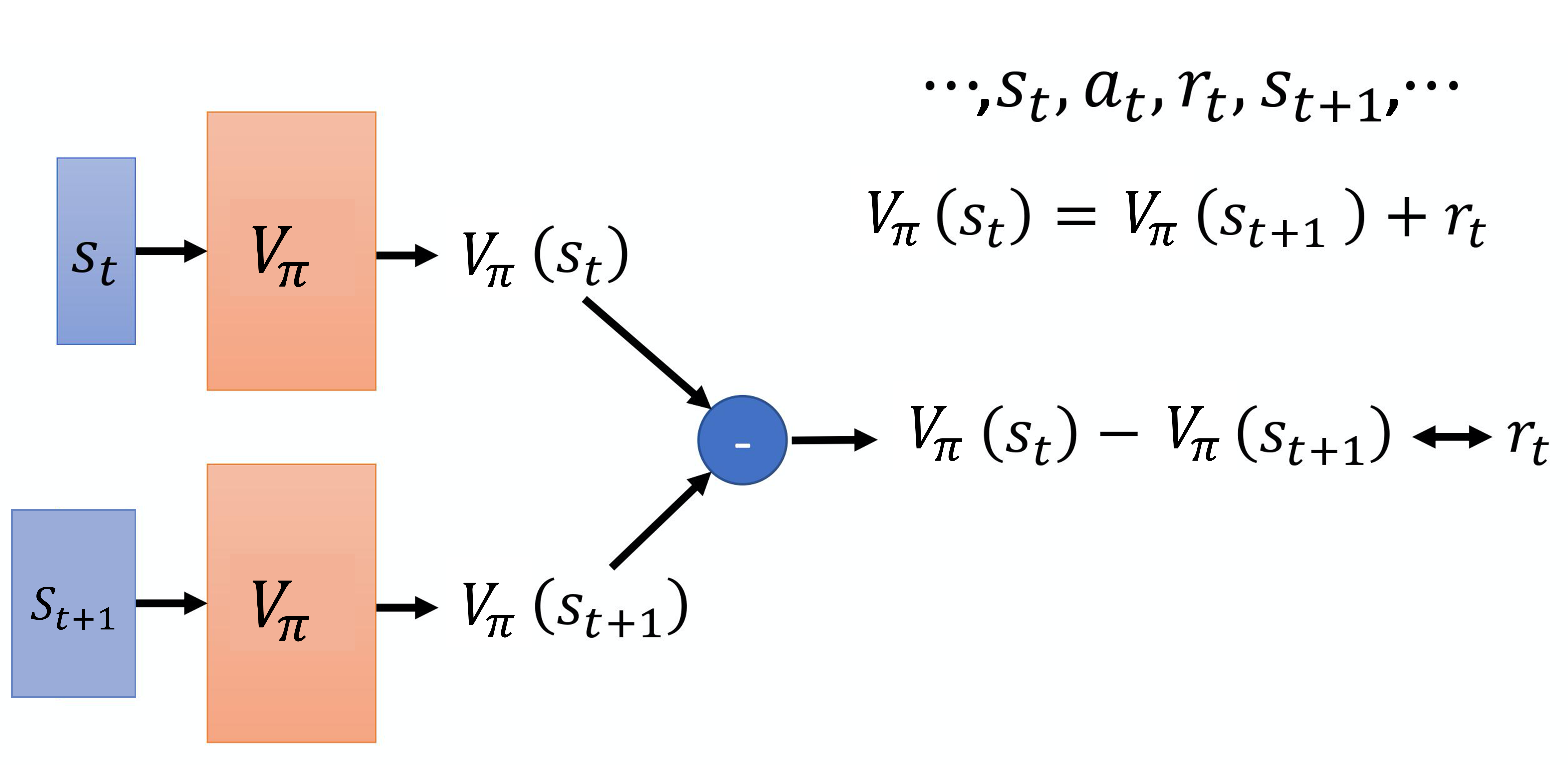
正因为这个“殊途同归”的多解性，即便学会了V函数，也很难直接根据最大V函数对应的状态$s$，反推出应采取的行为$a = \pi(s)$。因此，式子$\eqref{q-function}$中的Q函数$Q_\pi(s, a)$加入了行为输入，从而像式子$\eqref{det-policy}$一样反推出最优$a^* = \pi’(s)$：

$$
\begin{equation}
a^* = \pi’(s) = \arg\max_a Q_\pi (s, a)
\label{q-function-argmax}
\end{equation}
$$

注意，在Q函数中的输入行为$a$并不代表它一定会采取这个行为，而是将所有可能的行为$a$和当前的状态$s$都配对输入了一遍，看哪一个的价值$Q_\pi(s, a)$更大。根据Q函数的定义式$\eqref{q-function}$，$Q_\pi(s, a)$指的是采取当前行为之后的未来总收益，未来用的策略还是原来的策略$\pi$，只是当前强制用了一个行为$a$，这个行为是所有可能的行为之一，与策略$\pi$无关。

深度Q网络的学习方式，图片来自EasyRL在线版

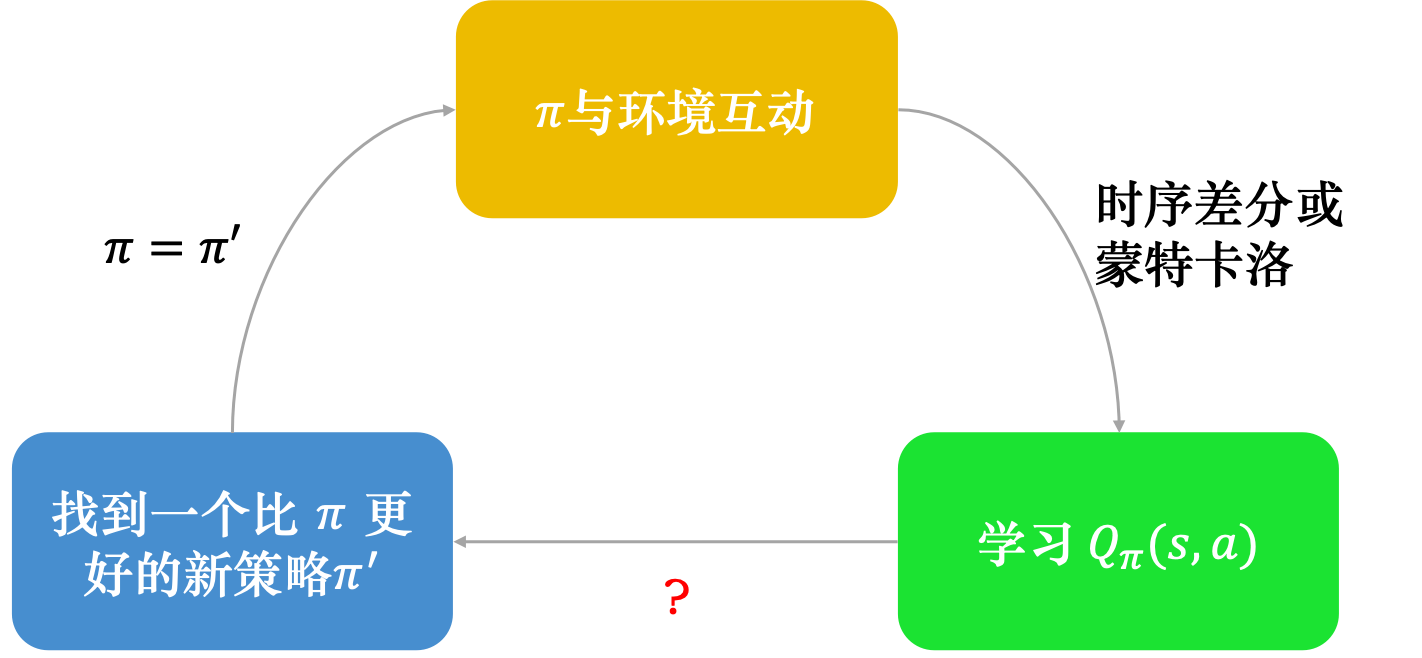
这个Q函数的学习方式，就可以是对策略的更新过程。那么问题来了，沿用原来策略$\pi$计算未来收益，找到了一个最好的$a^*$，这个只改变了一个行为的新策略$\pi’$为什么能够直接替换掉$\pi$？万一就因为改了这一个行为，未来总收益$V_{\pi’}(s) = Q_{\pi’}(s, a)$就比$V_{\pi}(s) = Q_\pi(s, a)$更差了呢。所以需要证明$V_{\pi}(s) \leq V_{\pi’}(s)$。首先改写式子$\eqref{q-function-argmax}$成$\max$形式：

$$
\begin{equation}
Q_\pi(s, \pi’(s)) = \max_a Q_\pi (s, a) \geq Q_\pi (s, a) = V_{\pi}(s)
\label{q-function-neq}
\end{equation}
$$

注意下标，计算未来收益时，策略都用原来的策略$\pi$，所以这个不等式是显然的，但$Q_\pi(s, \pi’(s)) \neq V_{\pi’}(s)$。根据式子$\eqref{q-function}$，展开$Q_\pi(s, \pi’(s))$，注意$G_t = r_t + V_\pi(s_{t+1})$，由不等式$\eqref{q-function-neq}$有$V_\pi(s_{t+1}) \leq Q_\pi(s_{t+1}, \pi’(s_{t+1}))$：

$$
\begin{equation}
\begin{split}
V_\pi (s)
& \leq Q_\pi(s, \pi’(s)) \\
& = \mathbb{E}_\pi \left[ r_t + V_\pi(s_{t+1}) | s_t = s, a_t = \pi’(s) \right] \\
& \leq \mathbb{E}_\pi \left[ r_t + Q_\pi(s_{t+1}, \pi’(s_{t+1})) | s_t = s, a_t = \pi’(s) \right] \\
& = \mathbb{E}_\pi \left[ r_t + r_{t+1} + V_\pi(s_{t+2}) | s_t = s, a_t = \pi’(s) \right] \\
& \cdots \\
& \leq \mathbb{E}_\pi \left[ r_t + r_{t+1} + r_{t+2} + \cdots + r_\mathrm{T} | s_t = s, a_t = \pi’(s) \right] \\
& = V_{\pi’}(s)
\end{split}
\label{q-function-proof}
\end{equation}
$$

个人认为，其实式子$\eqref{q-function-argmax}$是一个强假设，相当于$s$并不是一个特定的状态，而是可以随意替换成$s_t$或$s_{t+1}$都能成立的。相当于对任意状态$s$，都有只改一个$a$的新策略$\pi’$有更高的未来总收益$Q_\pi(s, \pi’(s))$，从而推出$\eqref{q-function-proof}$。

基于如此强的假设，策略$\pi$是怎么正确学习的呢？定义一个Q神经网络$Q_\pi(s, a)$，其输入是状态$s$和可能的行为$a$，而策略$\pi$是隐式编码在网络的权重当中的。参考前述的时间差分方法示意图，这个神经网络同样应当满足回归损失的约束：

$$
\begin{equation}
Q_\pi(s_{t}, a_{t}) = r_{t} + Q_\pi(s_{t+1}, \pi(s_{t+1}))
\end{equation}
$$

可以观察到，时间差分方法不需要采样出一个完整的轨迹$\tau$，每次只需要用当前的策略$\pi$与环境交互一次，采样出一组$\{ s_t, a_t, r_t, s_{t+1} \}$。如果能采到各种不同状态$s$，就可以找到一个新策略$\pi’$在各种状态下都能满足式子$\eqref{q-function-argmax}$。

经验重放技巧Experience Replay，图片来自EasyRL在线版

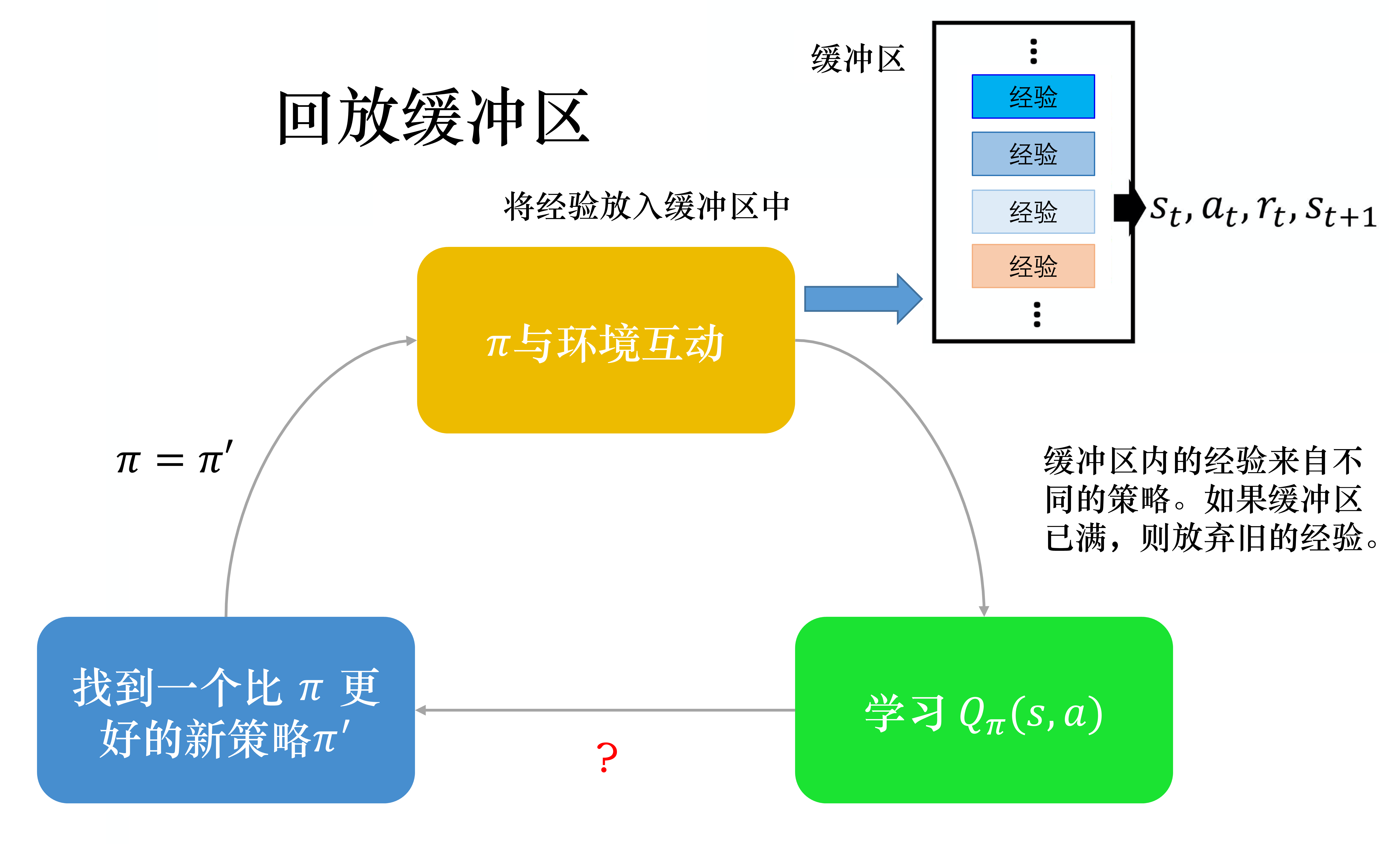
为了训练的稳定性，可以将$Q_\pi(s_{t+1}, a_{t+1})$设为一个定期更新的“目标网络”，不直接回传梯度，只有公式左边的Q网络预测值回传梯度。此外，为了减少当前策略与环境的交互的次数，将历史上的其他策略放入一个先入先出的队列中，不断将当前策略采样的$\{ s_t, a_t, r_t, s_{t+1} \}$放入这个队列，而最旧的策略不断出队，每次训练从这个队列中采样训练样本。何凯明提出的MoCo系列对比学习方法^[5]的动量更新模型+负样本队列，就很像“目标网络”+“经验重放”这两个技巧。

深度确定性策略梯度 Deep Deterministic Policy Gradient

对于深度Q网络DQN来说，在输入状态$s$的同时，还需要遍历输出各种可能的行为$a$对应的Q值$Q(s, a)$。如果当前任务的行为空间是离散的，例如有上下左右4种动作，那么相对容易遍历，只需定义Q网络的输出数量为4即可。但如果当前任务的行为空间是连续的，例如某个控制量的取值范围是$(0, 1)$，就没办法遍历所有的数值了。

深度确定性策略梯度Deep Deterministic Policy Gradient在深度Q网络上的改进，图片来自EasyRL在线版

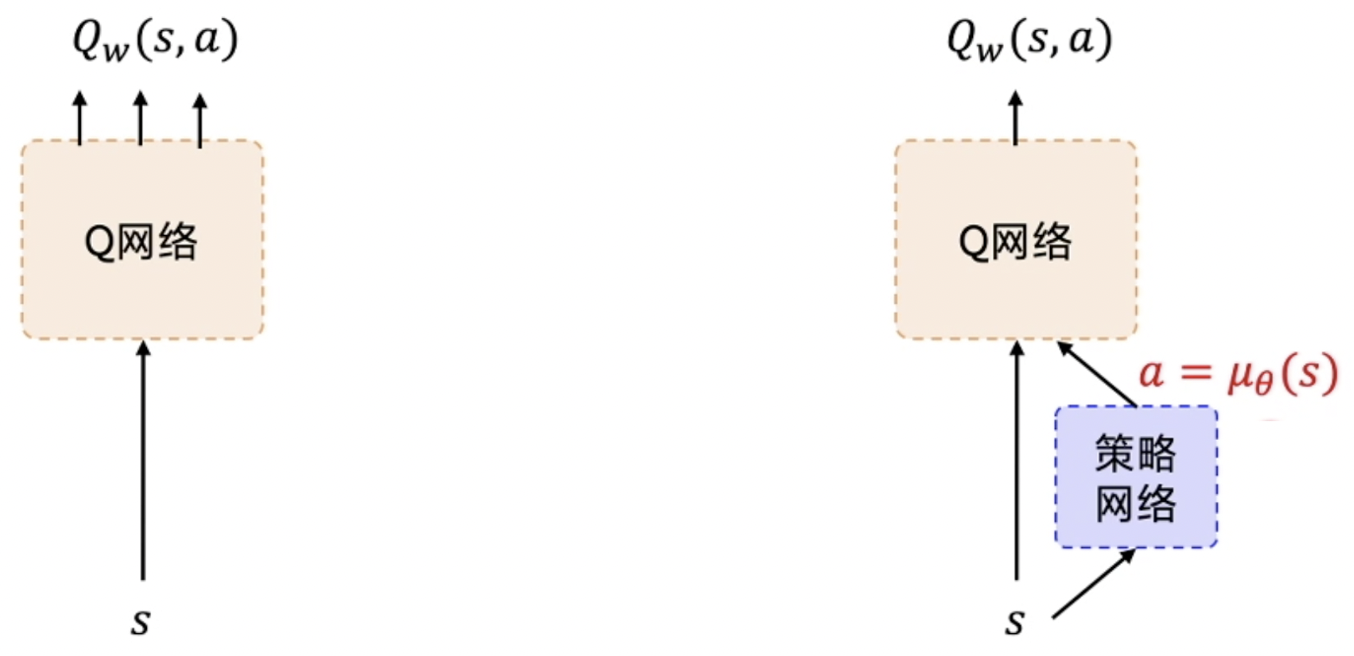
如果有一个额外的网络，帮助预测当前的$a$，使得深度Q网络获得了状态和行为2个输入，就可以只输出1个Q值代表$Q(s, a)$了。这个额外的网络就是策略梯度训练出来的网络。由于需要确定的行为$a$，式子$\eqref{pg-approx}$中基于随机概率$p_\theta(a_t|s_t)$的方法不太好用了，因此采用的确定性方法，全称就是深度确定性策略梯度Deep Deterministic Policy Gradient^[6]。

基于目标网络+经验重放的DDPG训练过程，图片来自EasyRL在线版

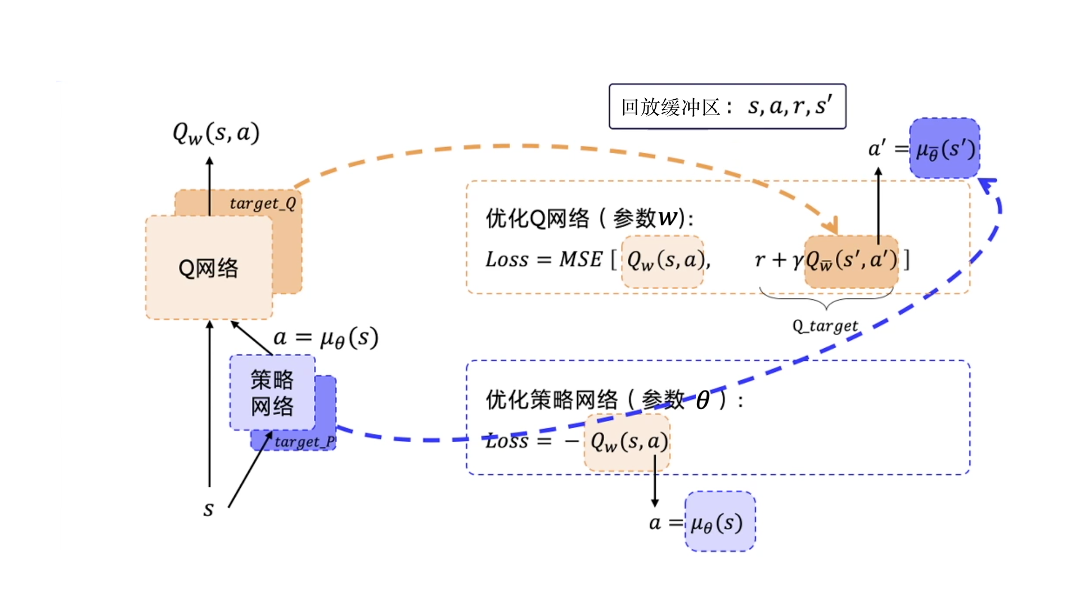
之前在近端策略优化的结尾、深度Q网络的开头，我们分别定义了演员Actor和评论家Crtic，在这里，演员变成了策略网络，评论家则是Q网络。继承了深度Q网络的目标网络技巧，分别定义目标Q网络$Q_\bar{w}(s’, a’)$和目标策略网络$a’ = \mu_\bar{\theta}(s’)$，两者参数定期从原网络更新。给定经验回放缓冲区$\{s, a, r, s’\} \sim \mathcal{D}$，基于时序差分方法的Q网络损失：

$$
\begin{equation}
\begin{split}
Q_w(s, a) & = r + \gamma Q_\bar{w}(s’, a’) \\
\Rightarrow \mathcal{L}_\mathrm{Q} & = \mathbb{E}_{\{s, a, r, s’\} \sim \mathcal{D}} \left\Vert Q_w(s, a) - (r + \gamma Q_\bar{w}(s’, a’)) \right\Vert^2_2 \\
& = \mathbb{E}_{\{s, a, r, s’\} \sim \mathcal{D}} \left\Vert Q_w(s, a) - (r + \gamma Q_\bar{w}(s’, \mu_\bar{\theta}(s’))) \right\Vert^2_2 \\
& \approx \frac{1}{N_s} \sum_s \left\Vert Q_w(s, a) - (r + \gamma Q_\bar{w}(s’, \mu_\bar{\theta}(s’))) \right\Vert^2_2
\end{split}
\end{equation}
$$

由于是在缓冲区$\mathcal{D}$上采样，所以是求期望。同样可以仿照式子$\eqref{pg-approx}$近似成求均值。同时，策略网络的优化目标是最大化“评论家”Q网络的输出价值，加一个负号就是最小化。为了与之前的随机性方法策略梯度区分，可以展开成积分形式：

$$
\begin{equation}
\begin{split}
\mathcal{L}_\mathrm{\mu} & = \mathbb{E}_{\{s, a, r, s’\} \sim \mathcal{D}} \left[ -Q_w(s, a) \right] \\
& = - \int \rho(s)Q_w(s, a) ds = - \int \rho(s)Q_w(s, \mu_\theta(s)) ds
\end{split}
\end{equation}
$$

可以看到，与策略梯度中的式子$\eqref{reward-expect}$不同，奖励$R(\tau)$变成了Q网络预测的Q值$Q_w(s, a)$，由策略模型预测的各行为概率$p_\theta(a_t|s_t)$构成的概率分布$p_\theta(\tau)$，变成了确定的$a = \mu_\theta(s)$，所以叫确定性策略梯度。期望里的概率值变为了在经验回放缓冲区上的采样$\rho(s)$（正常应该是$\rho(\{s, a, r, s’\})$）。和式子$\eqref{gradient-expect}$一样求梯度$\nabla = \frac{\partial}{\partial \theta}$，并和$\eqref{pg-approx}$一样近似求均值：

$$
\begin{equation}
\begin{split}
\nabla \mathcal{L}_\mathrm{\mu} & = - \nabla \int \rho(s)Q_w(s, \mu_\theta(s)) ds \\
& = - \int \rho(s) \nabla Q_w(s, \mu_\theta(s)) \nabla \mu_\theta(s) ds \\
& \approx \frac{1}{N_s} \sum_s \left[\nabla Q_w(s, \mu_\theta(s)) \nabla \mu_\theta(s) \right]\\
\end{split}
\end{equation}
$$

需要注意$Q_w(s, \mu_\theta(s))$是包含$\theta$的复合函数，复合函数求导$(f(g(x)))’ = f’(g(x)) \cdot g’(x)$。此外，虽然确定性的行为$a = \mu_\theta(s)$样本量需求小，但也导致在环境中的探索范围受限。对输出的行为$a$加入噪声，用$\mathrm{clip}(\cdot)$函数限制上下界：

$$
\begin{equation}
a = \mathrm{clip}(\mu_\theta(s) + \epsilon, a_\mathrm{low}, a_\mathrm{high}), \epsilon \sim \mathcal{N}(0, \sigma^2 I)
\end{equation}
$$

综上，从策略梯度PG到近端策略优化PPO、深度确定性策略梯度DDPG，强化学习与环境交互的成本在不断压缩：

• 一方面，PPO将策略梯度中需要反复采样的轨迹$\tau \sim p_\theta(\tau)$改为固定的$\tau \sim q_\hat{\theta}(\tau)$，从而使得对应轨迹的奖励$R(\tau)$固定，只需通过在固定轨迹上得到当前的$p_\theta(\tau)$，用重要性采样方法来赋予$p_\theta(\tau)$和$q_\hat{\theta}(\tau)$两个分布的权重。

• 另一方面，基于价值的方法DQN、DDPG直接不需要轨迹$\tau$，而是采用了时序差分方法，直接计算相邻两个状态$s_t$和$s_{t+1}$的价值Q函数之差$r_t$。目标模型技巧稳定了时序差分方法的训练过程，而经验重放技巧引入了历史交互的缓冲区队列$\{s, a, r, s’\} \sim \mathcal{D}$，进一步减少了当前策略下与环境的交互过程。

强化学习+大语言模型 RL-based Large Language Models

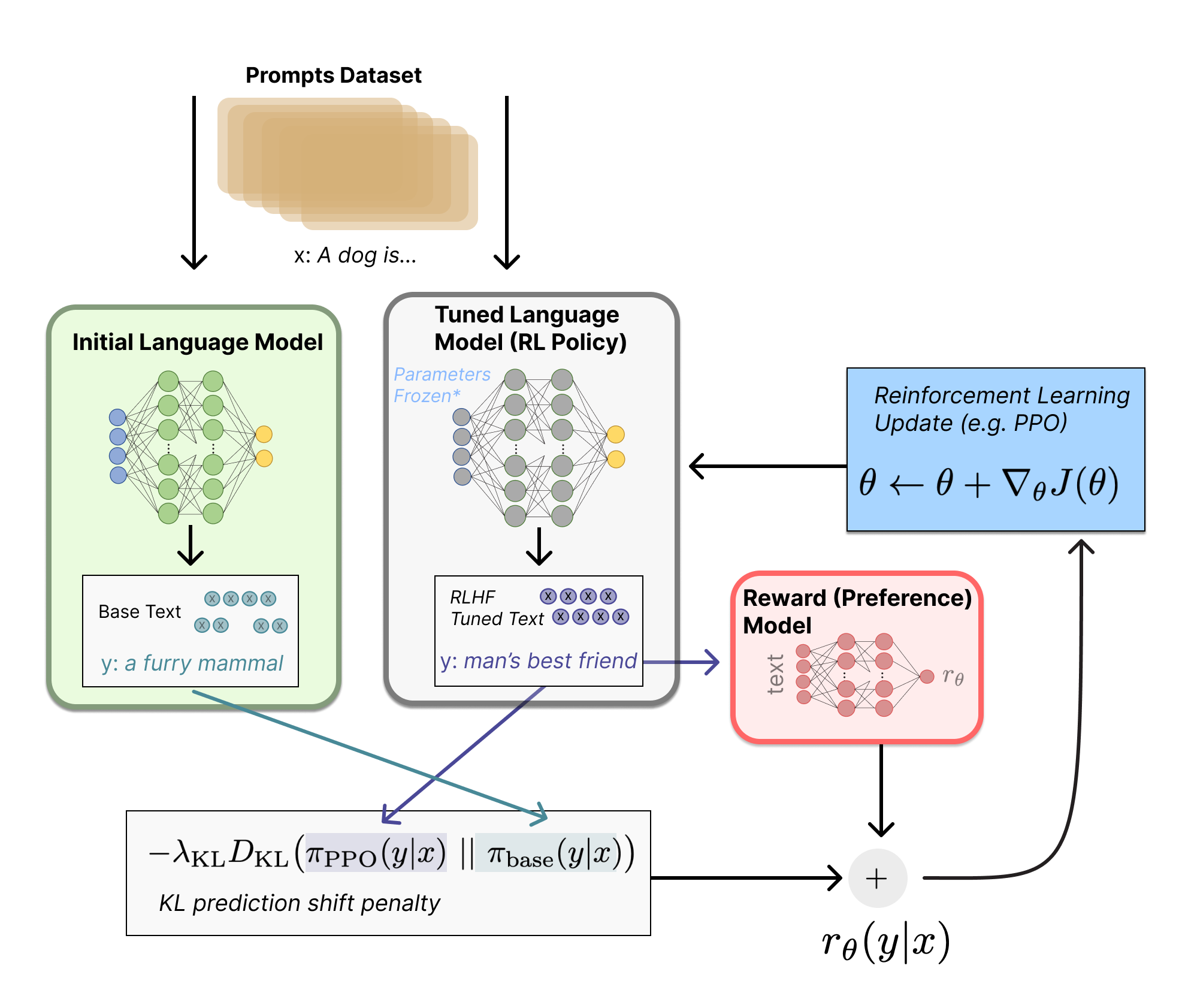
在近期火热的大语言模型领域，最经典的强化学习应用就是OpenAI发布的ChatGPT。在其第3个训练步骤中，采用了人类反馈的强化学习RLHF（Reinforcement Learning from Human-Feedback），是近端策略优化PPO的改进方法。

与式子$\eqref{ppo}$相比，奖励$R(\tau)$由一个独立的黑盒偏好模型给出（实际上是通过人类偏好排序得到的奖励），而非一个显式的公式；PPO中的KL散度约束，也不再是对权重进行约束，而是对模型输出的分布进行约束，但同样是一个固定权重、另一个学习权重。从基本定义来看，只要是能够通过分布约束，稳定强化学习的优化范围，都可以认为是PPO。

OpenAI提出的基于PPO的人类反馈的强化学习RLHF，图片来自HuggingFace

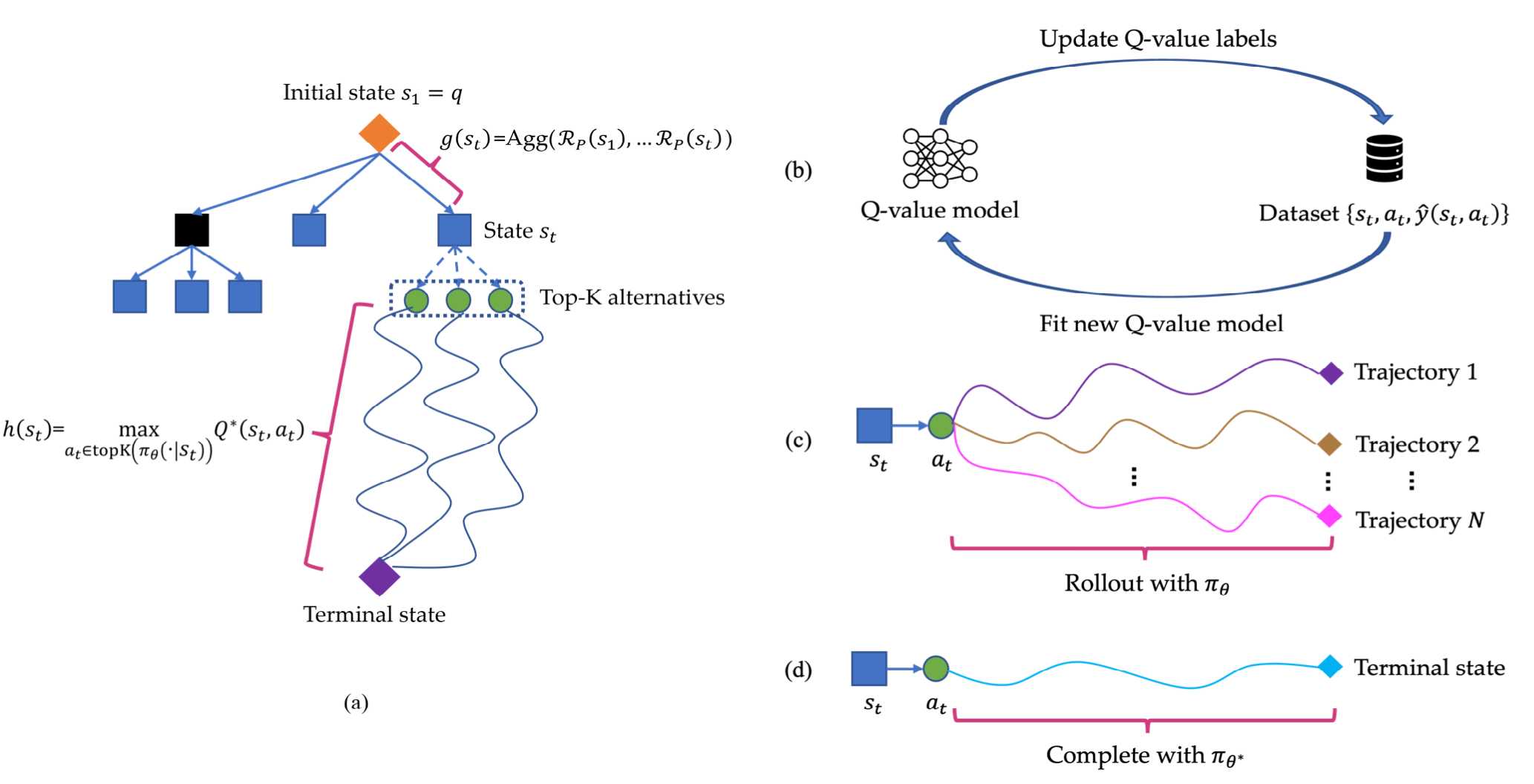
此外，颜水成团队在2024年6月份发表在arXiv上的文章Q*^[7]也尝试实现了传闻中OpenAI基于深度Q学习的下一代模型。该方法改进了训练结束后的自回归模型在推理过程中的采样方式，与之前提到的贪婪方法、集束搜索Beam Search方法不同，尝试训练了一个额外的Q-Value模型，预测模型在Top-K个采样序列上的Q值，选取Q值最大的序列作为结果。值得注意的是，该方法使用开源小模型作为基线方法，在使用Q*采样后，确实和传闻中一样能够在解数学题等逻辑推理问题上，超过多个闭源大模型。此外，结合Beam Search和Levin Tree Search等搜索方法、以及类似强化学习的过程监督奖励模型，华为蒙特利尔诺亚方舟实验室提出的MindStar^[8]采样方法，也能取得类似的“超越闭源大模型”的提升效果。

颜水成团队实现的基于深度Q学习的大语言模型采样方法Q*，图片来自论文原文^[7]

显然，大语言模型底层的自回归生成序列、轨迹的能力，不仅与强化学习的结合是如鱼得水的，而且还能扩展到其他领域，尤其是以深度学习三巨头Hinton团队提出的Pixel2Seq为代表的自回归视觉感知方法^[9]。在此基础上，谷歌DeepMind团队发表在ICML 2023上的工作“Tuning Computer Vision Models With Task Rewards”^[10]将不可微的评测指标，用式子$\eqref{prod-p}$中的策略梯度引入到了目标检测、图片描述生成等自回归方法中。当然，还有更多能够转化为自回归生成的研究或应用任务场景，等待着我们进一步去探索如何用强化学习进一步“强化”。

参考资料

• [1] Minsky M. Steps toward artificial intelligence[J]. Proceedings of the IRE, 1961, 49(1): 8-30.
• [2] 李宏毅. 深度强化学习. http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS18.html
• [3] Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction[M]. MIT press, 2018.
• [4] 王琦，杨毅远，江季. Easy RL：强化学习教程[M]. 人民邮电出版社, 2022.
• [5] He K, Fan H, Wu Y, et al. Momentum contrast for unsupervised visual representation learning[C]// Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2020: 9729-9738.
• [6] Continuous control with deep reinforcement learning[J]. 4th International Conference on Learning Representations, 2016.
• [7] Wang C, Deng Y, Lv Z, et al. Q*: Improving Multi-step Reasoning for LLMs with Deliberative Planning[J]. arXiv preprint arXiv:2406.14283, 2024.
• [8] Kang J, Li X Z, Chen X, et al. MindStar: Enhancing Math Reasoning in Pre-trained LLMs at Inference Time[J]. arXiv preprint arXiv:2405.16265, 2024.
• [9] Chen T, Saxena S, Li L, et al. Pix2seq: A Language Modeling Framework for Object Detection[C]//The Tenth International Conference on Learning Representations, 2022.
• [10] Pinto A S, Kolesnikov A, Shi Y, et al. Tuning computer vision models with task rewards[C]//International Conference on Machine Learning. PMLR, 2023: 33229-33239.