Notes About Functional Data Analysis

There is no branch of mathematics, however abstract,
which may not some day be applied to phenomena of the real world.
by Nikolai Ivanovich Lobachevsky

本文是关于函数型数据分析Functional Data Analysis的学习笔记
主要包括基函数展开、函数型数据分析、以及函数型神经网络Functional Neural Networks的一系列近期进展

前言 Introduction

1826年，在喀山大学的物理数学系学术会议上，罗巴切夫斯基首次提出了“非欧几何”。这一全新理论基于弯曲的几何空间，不引入欧几里得的“平行线公理”仍能自洽。然而从会上到会后，他收获的却是无尽的沉默、讽刺和质疑（这恰似如今学术会议多数“拒稿”的意见倾向），但他从未放弃在数学领域的探索，并留下了这句传世的名言：“不管数学的任一分支是多么抽象，总有一天会应用在这实际世界上”。

1854年，黎曼在哥廷根大学发表了演说《论几何基础中的假说》，正式确立了以黎曼几何为代表的非欧几何体系。1916年，爱因斯坦在《物理年鉴》发表了著名论文《广义相对论基础》，由黎曼几何得到启发，构建了基于质量产生时空弯曲的广义相对论。整整90年，罗巴切夫斯基的名言最终因自己的伟大理论而得到应验。

而在这锲而不舍的探索过程中，他还留下了另一个早期成果：B样条曲线B-Spline（全称为“基样条”Basis Spline，由舍恩伯格Isaac Jacob Schoenberg于1938年正式提出），这正是基函数展开方法Basis Function Expansion之一。

用“一组基函数+参数”表示复杂函数的思想，启发了近期热门的KAN网络^[1]通过学习1组B-Spline基函数的参数、得到任意形状的激活函数，也启发了通过学习2组基函数组合之间“参数到参数”的显式映射、得到“输入函数到输出函数”的回归分析方法：函数型数据分析Functional Data Analysis。

基函数展开 Basis Function Expansion

KAN方法示意图，通过步骤1学习任意形状的激活函数、无需学习权重参数，而非经典神经网络采用固定激活函数、学习权重参数。KAN还能通过通过步骤3~6，将学习到的激活函数逐个设定为已知函数，解析出显式、可嵌套的表达式
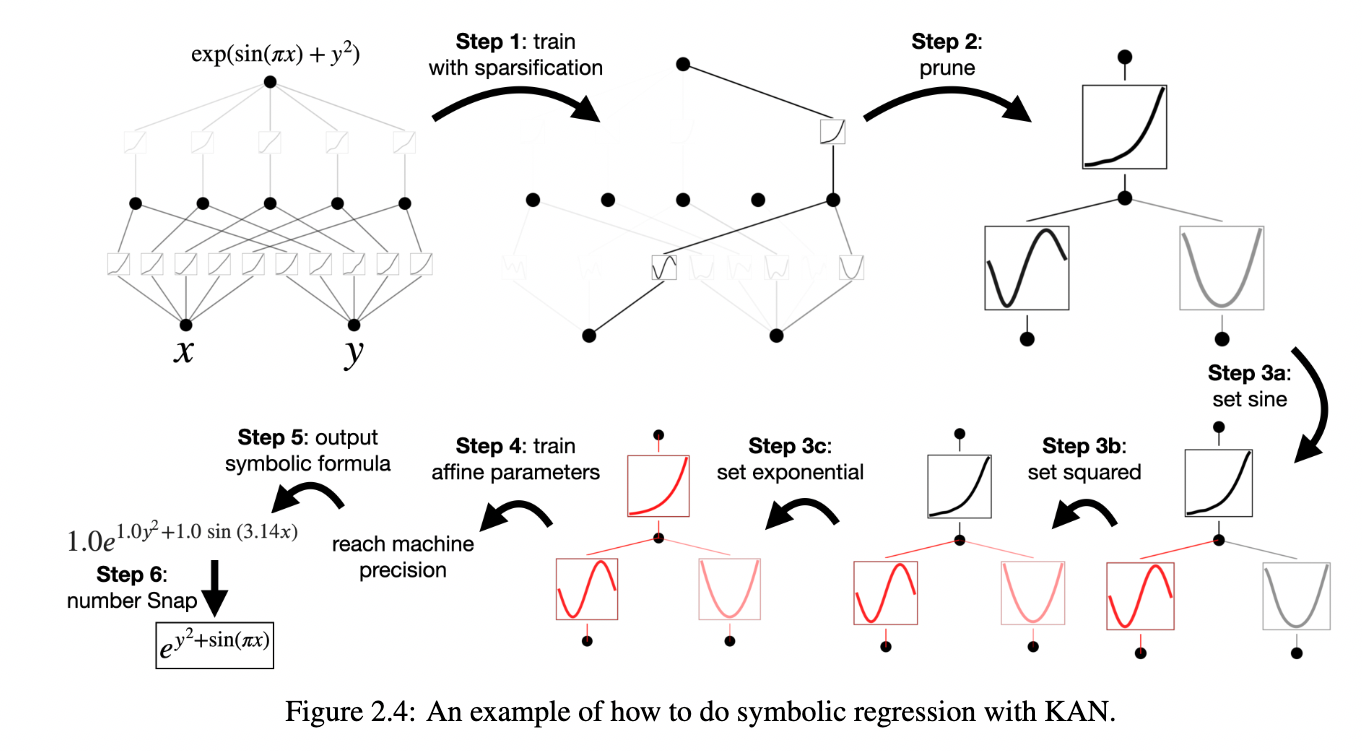
图片来自论文原文^[1]

之前的笔记主要强调了KAN基于任意形状激活函数的符号回归特性，但并未介绍KAN是如何学习到这些激活函数的。因此，这里以KAN采用的B样条曲线B-Spline为例，详细介绍如何用“一组基函数+参数”表示复杂函数。如下图所示，给定一组可学习权重参数$c_i$，以及一组固定基函数$B_i(x)$，B样条曲线$\mathrm{spline}(x)$通过两者线性加权求和，表示复杂函数$\phi(x)$：

$$
\begin{equation}
\phi(x) = \mathrm{spline}(x) = \sum_i c_i B_i(x)
\label{bspline}
\end{equation}
$$

KAN方法中的B-Spline示意图，右侧放大的是可学习激活函数的B-Spline曲线，其中横轴为不同的输入$x=t_i$取值，纵轴不同颜色代表了中心处于不同$t_i$的多个高斯核基函数$B_i(x)$，每个函数的线性参数为$c_i$，从而通过线性叠加组合成复杂函数$\phi(x)$
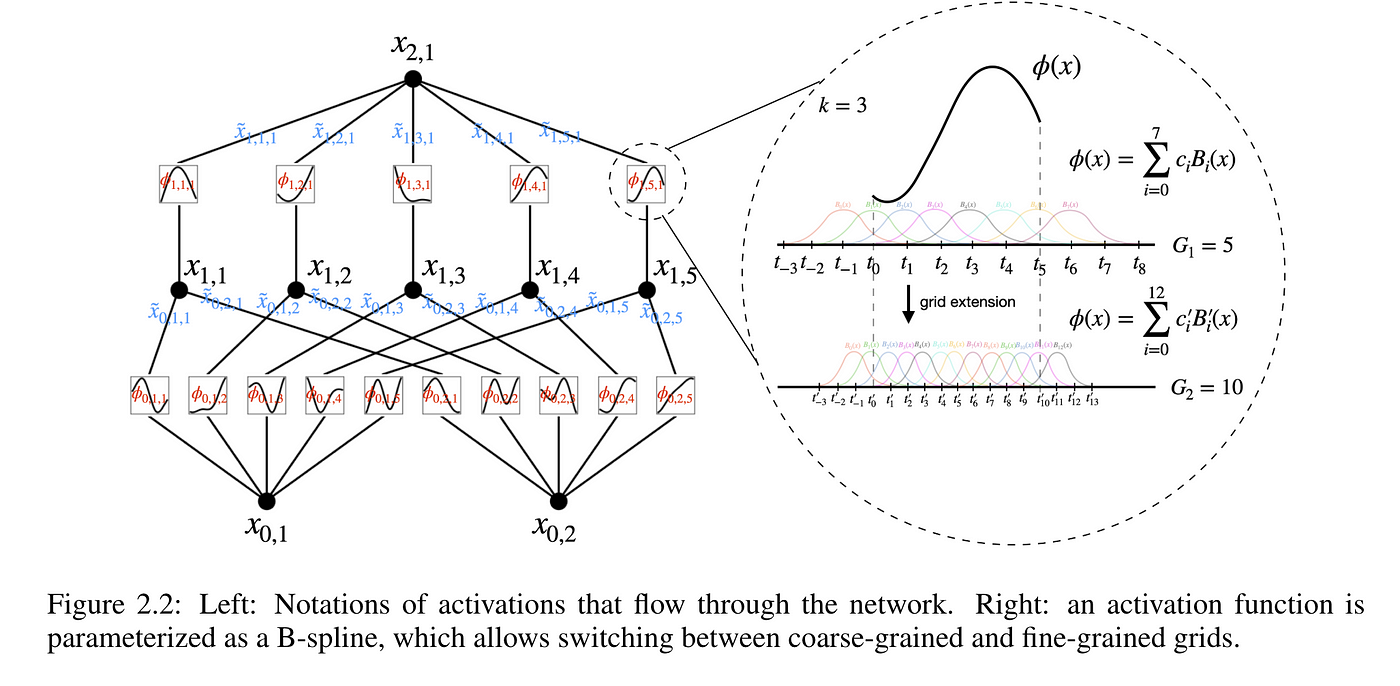
图片来自论文原文^[1]

B样条曲线采用了基于高斯函数形状的基函数，可以简单地理解为当前输入$x_i$对于最终输出的$\phi(x_i)$贡献程度就是$c_i$。如果该复杂函数具有较强的周期性质，也可以使用傅里叶基函数$\{\sin(i\omega t), \cos(i\omega t)\}$在频域上做加权求和。在时域层面，除了B-Spline之外，常用的还有薄板样条插值（Thin Plate Spline, TPS）等。此外，如果复杂函数$\phi(x)$有已知的若干个取值点$\left(x_j, \phi(x_j)\right)$，同样可以拟合出对应的参数$C=\{c_i\}$，从而实现对函数形状的插值。显然，基函数越多，插值或者表示（也即基函数展开）的精度就越高。

插一句题外话，如上述2张示意图所示，既然KAN网络与经典神经网络的区别如此之大，如何保证KAN网络也有相同的“万能近似理论”（Universal Approximation Theorem）呢？这就是其名字由来：Kolmogorov-Arnold表示定理。对于任意多元函数$f: [0, 1]^n \rightarrow \mathbb{R}$，输入为归一化到$[0,1]$区间的$x = \{ x_1, x_2, \cdots, x_p, \cdots, x_n \}$，都能表示为有限个单变量输入映射$\phi_{q, p}(x_p): [0,1] \rightarrow \mathbb{R}$，输出映射$\Phi_q(\cdot): \mathbb{R} \rightarrow \mathbb{R}$的函数组合和加法组合：

$$
\begin{equation}
f(x) = f(x_1, \cdots, x_n) = \sum_{q=1}^{2n+1} \Phi(\sum_{p=1}^{n} \phi_{q,p}(x_p))
\label{kart}
\end{equation}
$$

其中，单变量映射$\phi$和$\Phi$显然可以认为是任意形状的函数，可以是现有的激活函数、也可以是各种形状的其他函数，从而可以用式子$\eqref{bspline}$中的B样条曲线$\phi(x)$来表示这些单变量映射。这样，其模型结构也不再是基于多层感知机的经典神经网络$\tau(W^\top x+b)$。KAN论文原文强调，式子$\eqref{kart}$中对于KAN网络的隐藏层个数$2n+1$、层数深度2都可以自由调整。

函数型数据分析 Functional Data Analysis

对于KAN网络，学习1组B-Spline参数，即可得到任意形状的激活函数，而且其输入仍然是有限长度、可数个数$n$向量$x$，其输出亦然。但在实际应用中，有时需要构建“输入函数到输出函数”之间的映射关系，而在没有特殊定义的情况下，一个函数的定义域无论它是有界$(a, b)$、还是无界$(-\infty, +\infty)$的，其区间内的取值都是无限个数的，从而其值域的取值同样是无限个数的。

输入函数到输出函数的映射示意图，其中下方$x(s)$为输入函数，左侧$y(t)$为输出函数，可以看到如a）、b）、c）这样的多个输入函数值对多个输出函数值的正相关、负相关贡献程度
图片来自论文原文^[2]

这样一种“无限个值到无限个值”之间的映射关系，就无法用传统的n个值到m个值的实数空间映射$\mathbb{R}^n \rightarrow \mathbb{R}^m$来表示，从而需要引入形如$\mathbb{R}^\infty \rightarrow \mathbb{R}^\infty$的表示方式，但这样的表示方式无法体现是从哪个区间的无限个值到另一个区间的无限个值。因此，需要引入由某个固定区间内的所有函数构成的空间，这就是大名鼎鼎的泛函分析Funtional Analysis所研究的内容。

在泛函分析中，我们可以令区间为$(a, b)$的所有函数构成的空间为$\mathcal{U}(a, b)$。但是，我们无法确定$\mathcal{U}(a, b)$空间内函数应该有的性质。因此，我们先假设有某种简单的线性映射，可以表示函数f到g的映射关系，形如：

$$
\begin{equation}
g(t) = W(s) f(s) + b(t)
\label{wrong-fda}
\end{equation}
$$

其中，$t$和$s$分别属于不同的区间，也即$g \in \mathcal{U}(a, b)$和$f \in \mathcal{U}(c, d)$。显然，偏置的区间应该和输出的区间一样，也即$b \in \mathcal{U}(a, b)$，但比较难解决的是权重$W$应该长什么样，从直觉上看，它应该是所有$s$到所有$t$的一个全连接映射权重构成的、行和列都是无限长的矩阵，也就是影响输出$t$的不应该只有一个$s$，可以有多个。但式子$\eqref{wrong-fda}$这里显然只有一个特定的$s$到$t$的点对点映射，显然是错的。那么，我们可以构造一个对所有s的加权平均，又因为s是连续的，所以写成积分形式：

$$
\begin{equation}
g(t) = \sum_{s=c}^{d} W(s) f(s) + b(t) = \int_c^d W(s) f(s) ds + b(t)
\end{equation}
$$

但显然还是有问题，积分的结果是一个标量值，而非空间$\mathcal{U}(a, b)$里的函数。问题出在$W(s)$上，它只考虑了对$f(s)$的逐点加权，并未考虑对$g(t)$的逐点输出。代入一个确定的$s$，$W(s)$和$f(s)$都是一个标量，两者相乘再积分还是一个标量。所以，$W(s) \notin \mathcal{U}(a, b)$且$W(s) \notin \mathcal{U}(c, d)$，它应该是对每一点输入$s$，输出对所有$t$的权重，反过来，是对每一点输出$t$，给出所有输入$s$的权重，套用实数空间的矩阵定义，$W(s, t) \in \mathcal{U}(c, d) \times \mathcal{U}(a, b)$，且令$s \in \mathcal{S} = (c, d)$：

$$
\begin{equation}
g(t) = \int_\mathcal{S} W(s, t) f(s) ds + b(t)
\label{simple-fda}
\end{equation}
$$

虽然式子$\eqref{simple-fda}$的表达终于正确了，但是也引来了更多的问题：

1. 无限维破坏了内积的存在性，也即$\int_\mathcal{S} W(s, t) f(s) ds$这样的无限维的矩阵和无限维的向量相乘（内积），并不能像有限维那样保证存在，内积可能是无穷大的；

2. 如果要进行多次“函数到函数”的映射，也即$f(s)$可能也是另外两个无限维的矩阵、向量的内积后积分得到的，那么$f(s)$也应当保证另外两个矩阵、向量的内积是存在的；

3. 最本质的问题：我们知道无限维的向量就是一个函数，那么如何表示无限维的矩阵。

前2个问题其实就是在要求函数空间$\mathcal{U}$的性质，也就是空间内任意两元素$f$和$g$的内积满足

$$
\begin{equation}
\langle f, g \rangle=\int | f \cdot g | ds < \infty
\end{equation}
$$

显然地，如果$f = g$，那么有$L^2$-范数满足

$$
\begin{equation}
|| f ||^2 = \int | f \cdot f | ds = \int | f |^2 ds < \infty
\end{equation}
$$

在泛函分析中，称满足这一条件的空间为$L^2$-函数空间（$L^2$-Function Space），从而需要限定$\eqref{simple-fda}$中出现的各个元素满足：$g \in L^2\left(\mathcal{U}(a, b)\right)$、$f \in L^2\left(\mathcal{U}(c, d)\right)$、$b \in L^2\left(\mathcal{U}(a, b)\right)$、以及$W \in L^2\left(\mathcal{U}(a, b) \times \mathcal{U}(c, d)\right)$。

对于第3个问题，我们可以对矩阵$W$进行分解。由于其两个维度都可以视作函数，那么我们可以先将每个维度都用一组固定的基函数表示，输出维度用$U$个基函数$\Psi(t) = {\psi_u(t)}$、输入维度用$K$个基函数$\Phi(s) = {\phi_k(s)}$表示。那么，它们各自的加权求和参数可以写作$\Omega^\Psi = {\omega^\Psi_u} \in \mathbb{R}^{U}$和$\Omega^\Phi = {\omega^\Phi_k} \in \mathbb{R}^{K}$，这样未知数从无限个变成了有限个，同时令$\Theta = \Omega^\Psi\Omega^{\Phi \top}$，$\Theta \in \mathbb{R}^U \times \mathbb{R}^K$为参数相乘后的有限实数矩阵：

$$
\begin{equation}
\begin{split}
& \begin{split}
W(s, t) & = (\Phi(s) \Omega^\Phi) (\Psi(t) \Omega^\Psi)^\top \\
& = \Psi(t)^\top (\Omega^\Psi\Omega^{\Phi \top}) \Phi(s) \\
& = \Psi(t)^\top \Theta \Phi(s)
\end{split} \\
& \begin{split}
\Rightarrow g(t) & = \int_\mathcal{S} \Psi(t)^\top \Theta \Phi(s) f(s) ds + b(t) \\
& = \Psi(t)^\top \Theta \int_\mathcal{S} \Phi(s) f(s) ds + b(t) \\
& = \Psi(t)^\top \Theta \Phi^* + b(t)
\end{split}
\end{split}
\label{fda}
\end{equation}
$$

由于$\Psi(t)^\top \Theta$均与在$s \in \mathcal{S}$上的积分无关，因此可以提出到积分外。剩下的积分结果显然是一个有限维度的向量，因为是$K$个基函数中，每个基函数横轴上的每个点$s$的函数值、与输入函数$f$的每个点$s$的函数值相乘后求积分得到的，可以令$\Phi^* = \int_\mathcal{S} \Phi(s) f(s) ds \in \mathbb{R}^K$。

那么$\Phi^*$这样的运算表达了什么含义呢？其实相当于对输入函数$f(s)$做了编码操作（Encoding）。假设基函数采用的是B-Spline的高斯函数，那么逐点相乘、求积分后，得到的就是基函数中心所在位置上的函数值，从而将无限维的函数$f(s)\in L^2\left(\mathcal{U}(c, d)\right)$转换为了有限维的向量编码$\Phi^* \in \mathbb{R}^K$。反之，$\Psi(t)^\top \Theta$就是将这一向量解码（Decoding）回了无限维的函数。

在B-Spline中，基于高斯函数的基函数可以近似为尖峰函数，从而与输入函数逐点相乘、求积分，提取到的是基函数中心所在位置的输入函数值，从而完成了从无限维（定义域取值个数）函数到有限维（基函数个数）向量的编码操作（也即Encoding）
图片来自bsplines.org^[3]

总之，式子$\eqref{fda}$通过设置2组基函数$\Psi(t)$和$\Phi(s)$，将“函数到函数”的无限维映射$W(s, t)$，转换为了“参数到参数”的有限维映射$\Theta$，从而方便计算机对函数型数据之间映射的存储、以及对参数的优化学习。

这便是拉姆齐James O. Ramsay于21世纪初提出的函数型数据分析Functional Data Analysis（FDA）^[4]。它不仅限于“函数到函数”的回归问题，也能扩展到“函数到标量”（函数型回归模型Functional Linear Model^[5]），“函数到主成分”（函数主成分分析Functional Principal Component Analysis^[6]）等各类任务上。

虽然，随着深度学习的兴起，将离散化采集的时序数据直接输入到黑盒式的“序列到序列（Seq-to-Seq）”神经网络中成为了时序数据处理的主流，但FDA能够显式地给出两个函数之间的映射关系$\Theta$，从而直观地判断输入函数到输出函数之间的贡献程度，这是黑盒神经网络所无法轻易做到的，需要借助额外的可解释性方法作为辅助。

另外，对于一些本质上就是连续的、甚至是有解析式的序列，神经网络也只能做离散化采样处理（如果离散数据本身间隔不固定，还需要插值成连续函数后，再重新等间隔采样），得到固定间隔、固定个数的输入采样值，而非直接处理函数本身。

函数型神经网络 Functional Neural Networks

那么，如果神经网络也能像FDA这样显式、高效地处理函数型数据，就能兼顾可解释性、效率乃至性能了。于是，函数型神经网络Functional Neural Networks（FNN）应运而生。但是，经典的时序神经网络架构（RNN、Neural ODE、Transformer、Mamba等）都能够处理多变量时序数据，而插值后的多变量时序数据变成了多条输入函数$\mathrm{x}(s) = {x_j(s)}$。因此，首先需要将FDA扩展到支持多条输入函数：

$$
\begin{equation}
\begin{split}
y(t) & = b(t) + \sum_{j=1}^J \int_{\mathcal{S}_j} W_j(s, t)x_j(s)ds \\
& = b(t) + \Psi(t)^\top \Theta \sum_{j=1}^J \int_{\mathcal{S}_j} \Phi_j(s) x_j(s) ds
\end{split}
\label{multi-fda}
\end{equation}
$$

简单地，2024年NeurIPS论文FUNNEL^[2]提出，基于式子$\eqref{fda}$和$\eqref{multi-fda}$将有限维参数$\Theta$替换为经典神经网络，从而方便地处理有限维输入和输出，但这一结构依赖于预定义用于编码和解码的基函数，若基函数选取不妥则性能提升存在一定的瓶颈。2020年IEEE Big Data论文^[7]也提出了基于函数式主成分分析FPCA+经典神经网络代替$\Theta$的类似版本。

图（a）提出了将FDA中可解释的有限维映射$\Theta$替换为经典神经网络的方法，由于是可解释+黑盒方法故称之为半结构化架构。图（b）则提出直接采用FNN，从而无需依赖预定义用于编码和解码的基函数，且输出仍然是函数，可直接与FDA的输出结果进行加法融合
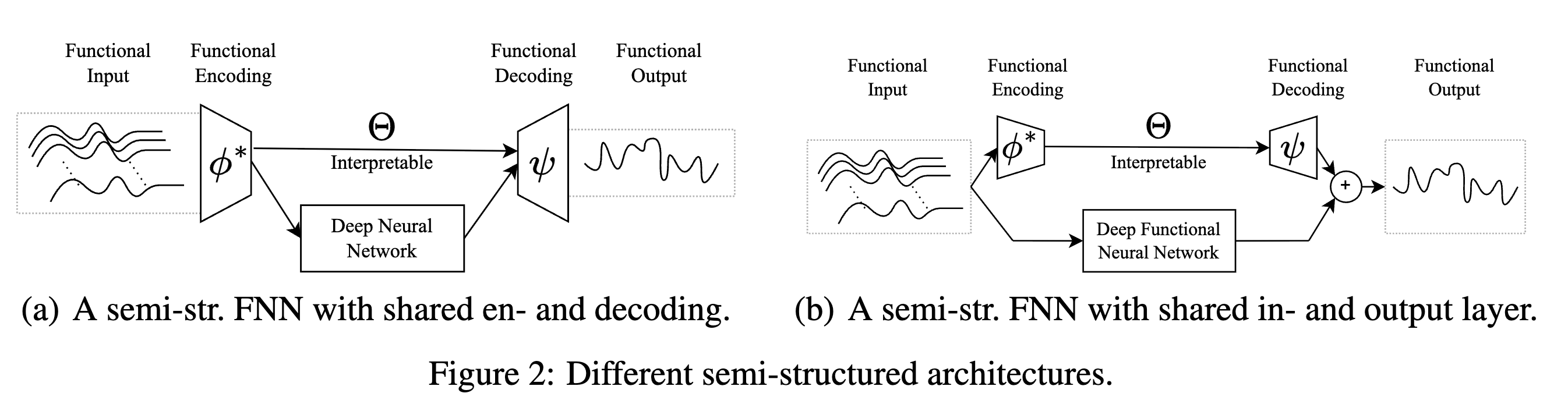
图片来自论文原文^[2]

从直觉上来看，将式子$\eqref{multi-fda}$中的$W_j$和$b$直接转换为可学习的参数，先不考虑这些函数空间中的元素如何在计算机上表示，加上激活函数$\tau$即可转换为函数型神经网络FNN：

$$
\begin{equation}
h^{(l)}_k(t) = \tau\left( b^{(l)}_k(t) + \sum_{m=1}^M \int W^{(l)}_{m,k}(s, t)h^{(l-1)}_m(s)ds \right)
\label{fnn-overall}
\end{equation}
$$

其中，$l$表示当前为第$l$层网络，$k$表示当前网络的第$k$维特征输出，$m$表示上一层网络的第$m$维特征输出。$h^{(l-1)}_m$为上一层网络的特征，输入层$h^{(0)}_m = x_m$。2024年的综述^[8]总结多种FNN实现，包括基于基函数内积、基函数展开的方法等。

基于基函数内积的方法 Basis-Function Product-based FNNs

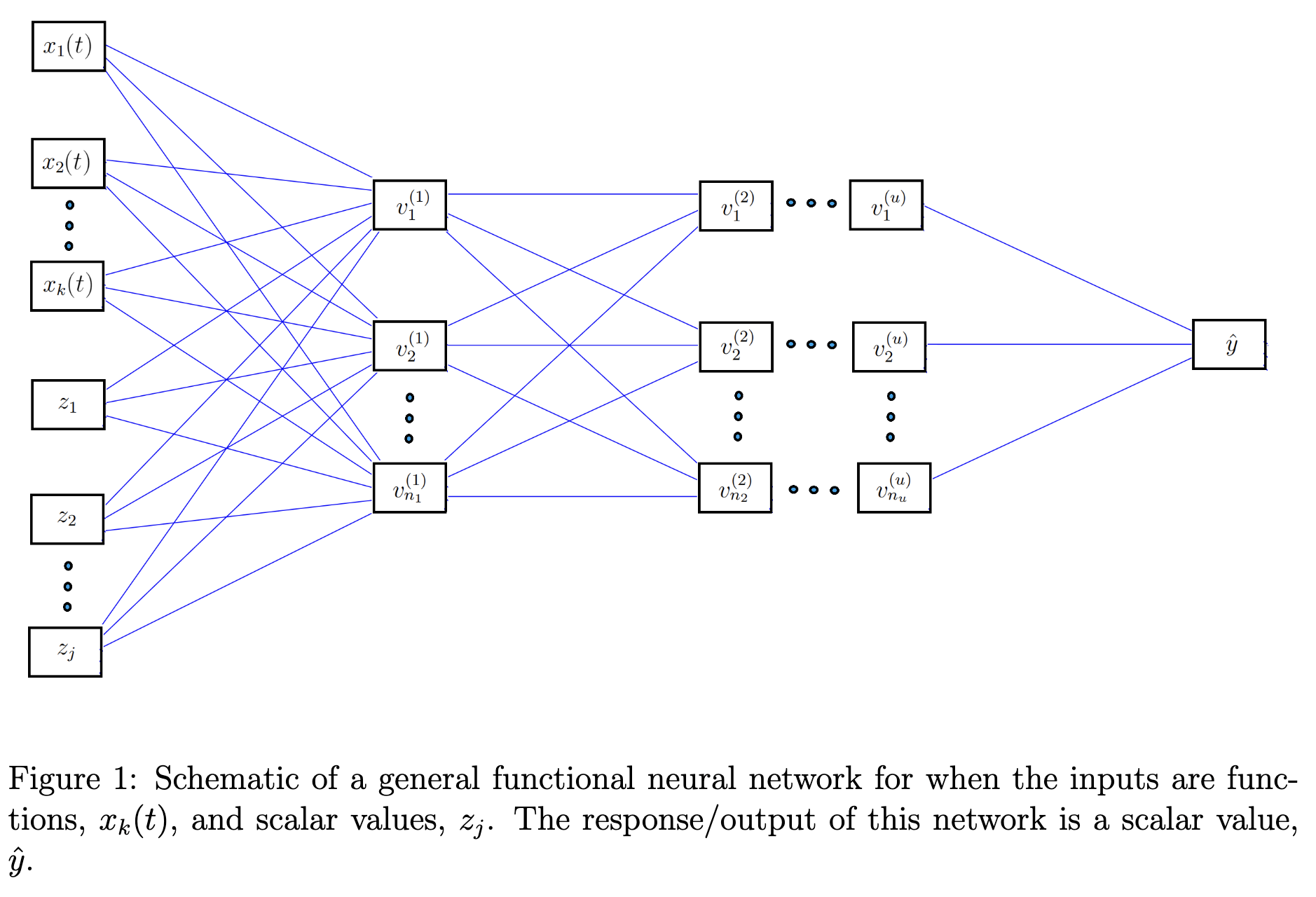
如上图所示，论文^[9]在网络的第一层直接尝试将函数型数据与基函数做内积，从而转换为有限维度，且无需考虑反向传播的积分可微问题，可以作为输入网络前的数据预处理步骤：

$$
\begin{equation}
\begin{split}
h_k^{(1)} & = \tau\left( \int_\mathcal{S} \beta_k(s) x(s) ds + b^{(1)}_k \right) \\
& = \tau\left( \int_\mathcal{S} \sum_{m=1}^{M} c_{m,k} \phi_{m,k}(s) x(s) ds + b^{(1)}_k \right) \\
& = \tau\left( \sum_{m=1}^{M} c_{m,k} \int_\mathcal{S} \phi_{m,k}(s) x(s) ds + b^{(1)}_k \right)
\end{split}
\label{jcg}
\end{equation}
$$
显然，基函数$\phi_{m,k}$与输入函数$x$逐点相乘、积分后，得到的结果是一个标量，再与基函数的参数加权求和，仍然是一个标量。从而后续网络层可以直接使用经典网络，其实类似于上图（a）的结构，基函数$\Phi$负责处理输入函数。这里为了简洁表达，省略了多条输入函数$\mathrm{x}(s) = {x_j(s)}$的情况。

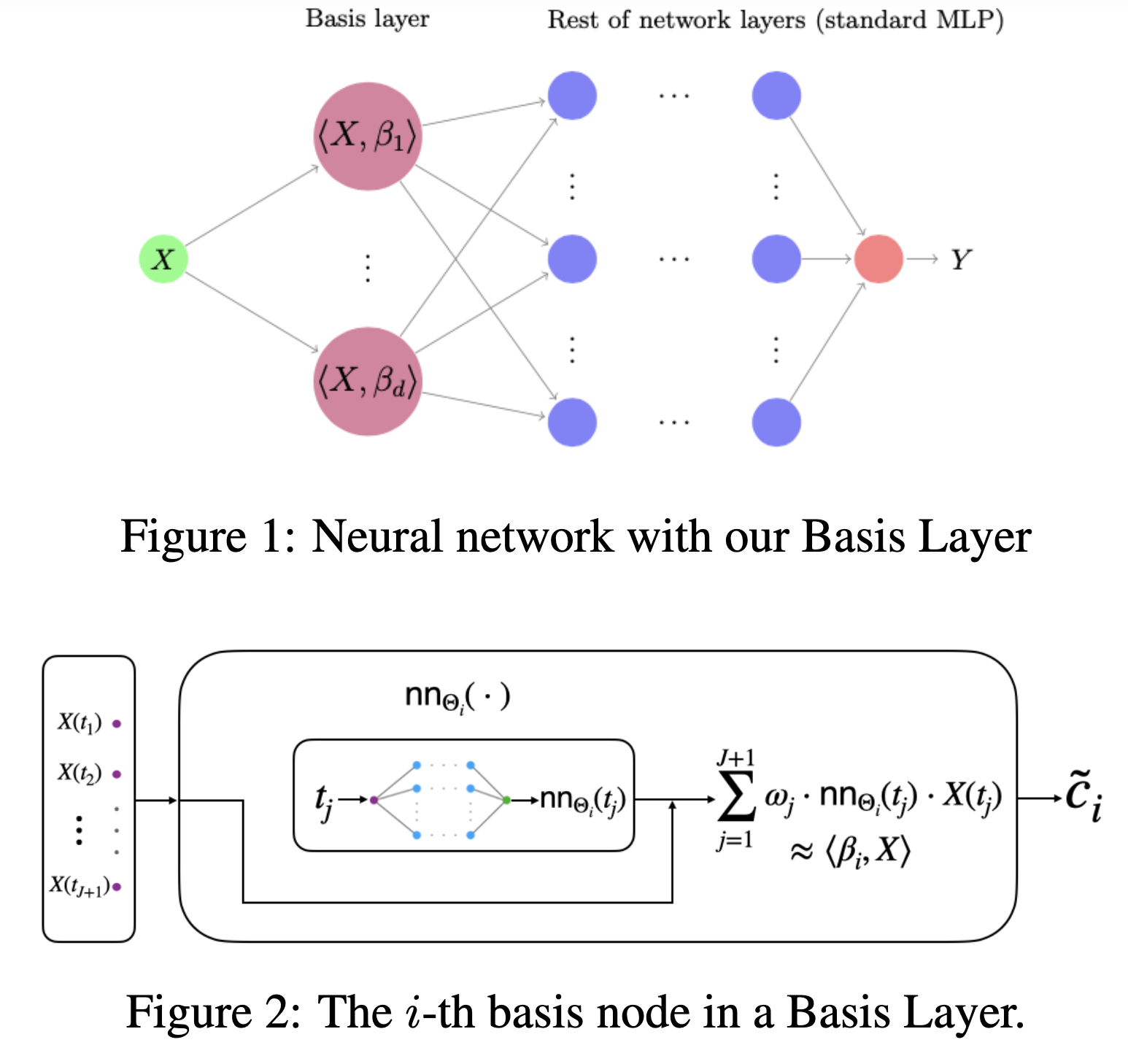
类似地，如上图所示，ICML2021论文AdaFNN^[10]提出了额外的动态神经网络$\mathrm{NN}_\Theta(s)$，将当前时刻$s$作为输入条件，近似输出当前时刻基函数的值$\phi(s)$，从而近似于$\langle \beta_k(s), x(s) \rangle$，除第一层之外的后续网络层同样使用经典神经网络，其中内积的推导可以套用式子$\eqref{jcg}$：

$$
\begin{split}
h_k^{(1)}
& = \tau\left( \langle \beta_k(s), x(s) \rangle + b^{(1)}_k \right) \\
& = \tau\left( \int_\mathcal{S} \beta_k(s) x(s) ds + b^{(1)}_k \right) \\
& = \tau\left( \sum_{m=1}^{M} c_{m,k} \int_\mathcal{S} \phi_{m,k}(s) x(s) ds + b^{(1)}_k \right) \\
& \approx \tau \left( \sum_{m=1}^{M} c_{m,k} \sum_{j=1}^J \mathrm{NN}_{\Theta_{m,k}}(s_j) \cdot x(s_j) + b^{(1)}_k \right) \\
& = \tau \left( \sum_{m=1}^{M} \sum_{j=1}^J \omega_{j,k} \cdot \mathrm{NN}_{\Theta_{m,k}}(s_j) \cdot x(s_j) + b^{(1)}_k \right)
\end{split}
$$

与AdaFNN类似，IJCNN2002论文FDAMLP^[11]同样观察到了式子$\eqref{fnn-overall}$中函数空间中的元素难以在计算机上表示的问题，提出采用一个基于有限维参数的回归模型（Parametric Regressor，可以是经典神经网络）$F$替代无限维权重，给定K个有限维参数$w = \{w_1, \cdots, w_k\}$，回归模型$F_i(w_i, \cdot)$接受参数$w_i\in \mathbb{R}^j$和当前时刻多维输入$x \in \mathbb{R}^n$，输出标量$\mathbb{R}$，也即$F_i : \mathbb{R}^j \times \mathbb{R}^n \rightarrow \mathbb{R}$。

实际上，这也是将式子$\eqref{fnn-overall}$的无限维权重$W$降级成了类似基函数的$F$，其中$w_i$相当于基函数的参数，$x$给定了当前时刻多维输入信息，相乘求积分（函数内积$\langle F, g \rangle = \int F \cdot g d\mu$）后得到的是一个标量，后续再叠加多层网络也只能是经典神经网络，因此论文只构建了一个简单的单层MLP网络：

$$
\begin{split}
h(g, w) = \sum_{i=1}^k a_i \tau\left( b_i + \int F_i(w_i, x) g(x) d\mu(x) \right)
\end{split}
$$

其中，$\mu(x)$写作在$\mathbb{R}^n$上的有限Borel测度，实际上就是在求当前时刻多维输入信息对应的时间戳，可以省略时间戳下标$x = X_l$，$l\in \mathbb{N}$。另外$F: \mathcal{W} \times \mathbb{R}^n \rightarrow \mathbb{R}$中，$\mathcal{W}$为$\mathbb{R}^j$上的紧集，意思是有限维参数集合$w$并不能覆盖整个$\mathbb{R}^j$空间内的所有元素，只能覆盖有限的K个。这些都是测度论的相关概念，但总归能翻译为白话。

总之，上述方法只是在输入阶段采用了纯白盒FDA^[9]、结合了神经网络的灰盒FDA^[10][11]，后续仍然采用黑盒的经典神经网络，所以并没有实现真正的FDA的可解释性，显式建模输入函数对输出结果的贡献。此外这些方法也无法实现“函数到函数”的映射，因为后续输出依赖于经典神经网络，只能是有限维度，不能是无限维度的函数。

基于基函数展开的方法 Basis-Function Expansion-based FNNs

基于基函数内积方法与基函数展开方法的区别，前者在第一层就通过函数内积的形式得到了有限维特征向量，后者始终采用有限维特征向量表示无限维函数
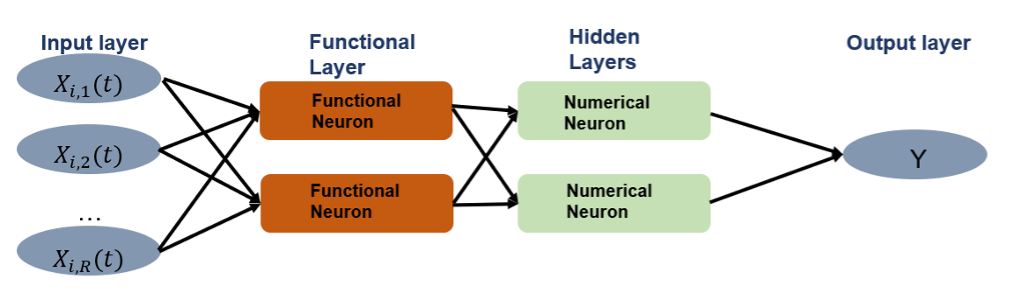
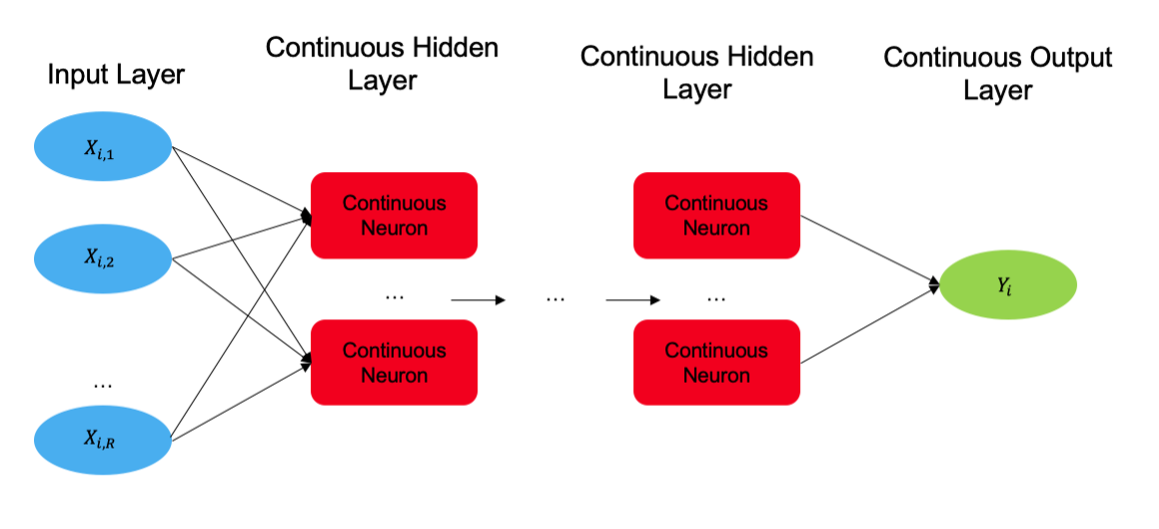
图片来自论文原文^[12][13]

为了实现“函数到函数”的映射，必须使得第一层FNN的输出仍然是一个函数，就像式子$\eqref{fnn-overall}$那样。但是，现代神经网络建立在有限维度张量Tensor的前向运算、反向传播操作上，所以必须有一种近似手段，将无限连续的积分操作，转换成有限维度的张量操作。

2021年，Aniruddha Rajendra Rao等人总结了上述基于基函数内积方法的不足，首次提出了函数式直接神经网络Functional Direct Neural Network（FDNN，即式子$\eqref{fnn-overall}$）、以及更容易实现的函数式基神经网络Functional Basis Neural Network（FBNN），论文的两个版本均于2023年正式发表^[12][13]。FBNN的“基”正是前述章节中的“基函数展开”，并同样采用FDA中对无限维矩阵的展开方式，也即式子$\eqref{fda}$。

首先，我们从简单的偏置$b^{(l)}_k(t)$入手，之前式子$\eqref{fda}$没有对它进行展开，是因为它本身可以分为有解析式、无解析式两种情况，有明确解析式只需要优化其中的预设参数，无解析式同样需要用基函数+参数表示。在神经网络中显然属于后者。给定一组基函数$v^*(t) = \left([v^*_b(t)]^B_{b=1}\right)^\top$和对应参数$B^{(l)}_k = [b^{(l)}_{k, b}]^B_{b=1}$：

$$
\begin{equation}
b^{(l)}_k(t) = \sum_{b=1}^B b^{(l)}_{k, b} v^*_b(t) = B^{(l)}_k v^*(t)
\label{b-basis}
\end{equation}
$$

对于式子$\eqref{fnn-overall}$中的权重$W^{(l)}_{m,k}(s, t)$，与式子$\eqref{fda}$类似，给定两组基函数$v_c(t)$和$v_d(s)$，以及它们的权重映射矩阵$\Theta^{(l)}_{m,k} = [\theta^{(l)}_{m,k,c,d}]_{c=1,d=1}^{C,D}$：

$$
\begin{equation}
W^{(l)}_{m,k}(s, t) = \sum_{c=1}^{C} \sum_{d=1}^{D} \theta^{(l)}_{m,k,c,d} v_c(t) v_d(s)
\label{w-basis}
\end{equation}
$$

将上述基函数展开式子$\eqref{b-basis}$、$\eqref{w-basis}$代入到理想的FNN式子$\eqref{fnn-overall}$中，即可得到FBNN的表达式，和FDA的式子$\eqref{fda}$一样，令$\Phi^{(l)}_{m,d}=\int v_d(s) h^{(l-1)}_m(s)ds$，则$\Phi^{(l)}_{m} = [\Phi^{(l)}_{m,d}]_{d=1}^{D}$：

$$
\begin{equation}
\begin{split}
h^{(l)}_k(t) & = \tau\left( b^{(l)}_k(t) + \sum_{m=1}^M \int W^{(l)}_{m,k}(s, t)h^{(l-1)}_m(s)ds \right) \\
& = \tau\left( B^{(l)}_k v^*(t) + \sum_{m=1}^M \int \sum_{c=1}^{C} \sum_{d=1}^{D} \theta^{(l)}_{m,k,c,d} v_c(t) v_d(s) h^{(l-1)}_m(s)ds \right) \\
& = \tau\left( B^{(l)}_k v^*(t) + \sum_{m=1}^M \sum_{c=1}^{C} \sum_{d=1}^{D} \theta^{(l)}_{m,k,c,d} v_c(t) \int v_d(s) h^{(l-1)}_m(s)ds \right) \\
& = \tau\left( B^{(l)}_k v^*(t) + \sum_{m=1}^M \sum_{c=1}^{C} \sum_{d=1}^{D} \theta^{(l)}_{m,k,c,d} v_c(t) \Phi^{(l)}_{m, d} \right) \\
& = \tau\left( B^{(l)}_k v^*(t) + \sum_{m=1}^M \Theta^{(l)}_{m,k} v(t) \Phi^{(l)}_{m} \right) \\
\end{split}
\end{equation}
$$

可以看到，需要学习的有限维参数是$B^{(l)}_k \in \mathbb{R}^B$和$\Theta^{(l)}_{m,k} \in \mathbb{R}^C \times \mathbb{R}^D$，由于基函数无可学习参数，由基函数构成的$\Phi^{(l)}_{m}$也同理，因此在反向传播求梯度偏导的时候，均可作为相乘的系数提出来，令$\tau’$为激活函数的导数：

$$
\begin{equation}
\begin{split}
& \frac{\partial h^{(l)}_k(t)}{\partial B^{(l)}_k} = \tau’\left( B^{(l)}_k v^*(t) + \sum_{m=1}^M \Theta^{(l)}_{m,k} v_c(t) \Phi^{(l)}_{m} \right) \times v^*(t) \\
& \frac{\partial h^{(l)}_k(t)}{\partial \Theta^{(l)}_{m,k}} = \tau’\left( B^{(l)}_k v^*(t) + \sum_{m=1}^M \Theta^{(l)}_{m,k} v(t) \Phi^{(l)}_{m} \right) \times v(t) \Phi^{(l)}_{m}
\end{split}
\end{equation}
$$

但是和FDA一样，上述基函数展开操作只解决了“无限维参数优化困难”的问题，并未解决第一层网络开始就要求的“中间特征需要无限维连续”的问题。由于FDNN、FBNN^[14][15]、以及2024年NeurIPS论文FUNNEL^[2]在GitHub上的开源代码^[18]都是用R语言实现的，这里列出另一篇ICML2023的后续工作FuncConv^[16]（论文将FBNN称为FuncDense）在GitHub上的Python开源代码^[17]，完整内容请参见GitHub仓库。其中，Legendre指的是勒让德基函数，是一组在$(-1, 1)$区间上、带有微分项的多项式函数，给定输入参数$l$，表达式如下：

$$
P(l, x) = \frac{1}{2^l l!} \frac{d^l}{dx^l} (x^2 - 1)^l
$$

def define_basis(
        basis_type: str,
        n_functions: int,
        resolution: Union[int, tuple]
) -> tf.Tensor:
    """
    Define basis functions - called when functional layer is initialized. The
    basis functions are defined at discrete time steps. The number of time
    steps is specified by the resolution.
    Note: The resolution might be given as int if the basis functions depend on
    a single variable. If the basis functions depend on multiple variables, a
    tuple is required.

    :param basis_type: Type of basis, given as string. Currently available:
        - 'Fourier'
        - 'Legendre'
    :param n_functions: Number of basis functions.
    :param resolution: Resolution of the basis - the basis functions are
        defined at equidistant points.
    :return: Basis as tf.Tensor with shape (resolution, n_functions).
    """
    if isinstance(resolution, int):
        resolution = (resolution,)

    if basis_type == 'Legendre' and len(resolution) == 1:
        support = np.linspace(-1, 1, resolution[0])
        basis = [legendre(i)(support) for i in range(n_functions)]

    elif basis_type == 'Fourier' and len(resolution) == 1:
        support = tf.linspace(0, 1, resolution[0])
        factor = tf.cast(tf.sqrt(2.0), dtype=tf.float64)
        basis = [factor * tf.math.sin(pi * (i + 1) * support) if i % 2 == 1
                 else factor * tf.math.cos(pi * i * support) if i > 0
                 else tf.ones_like(support)
                 for i in range(n_functions)]

    else:
        raise NotImplementedError(f"Basis type {basis_type} not implemented.")

    basis = tf.stack(basis, axis=-1)
    basis = tf.cast(basis, dtype=tf.float32)

    return basis

可以看到，通过规定resolution分辨率长度，基函数可以通过linspace函数在有区间（例如代码中的$(0,1)$、$(-1,1)$等）时序维度上进行等间隔采样得到，从而使得中间任意特征的维度都是有限的，实现了对现有深度学习框架的兼容（这里使用的是Tensorflow，理论上PyTorch也能改写后兼容）。

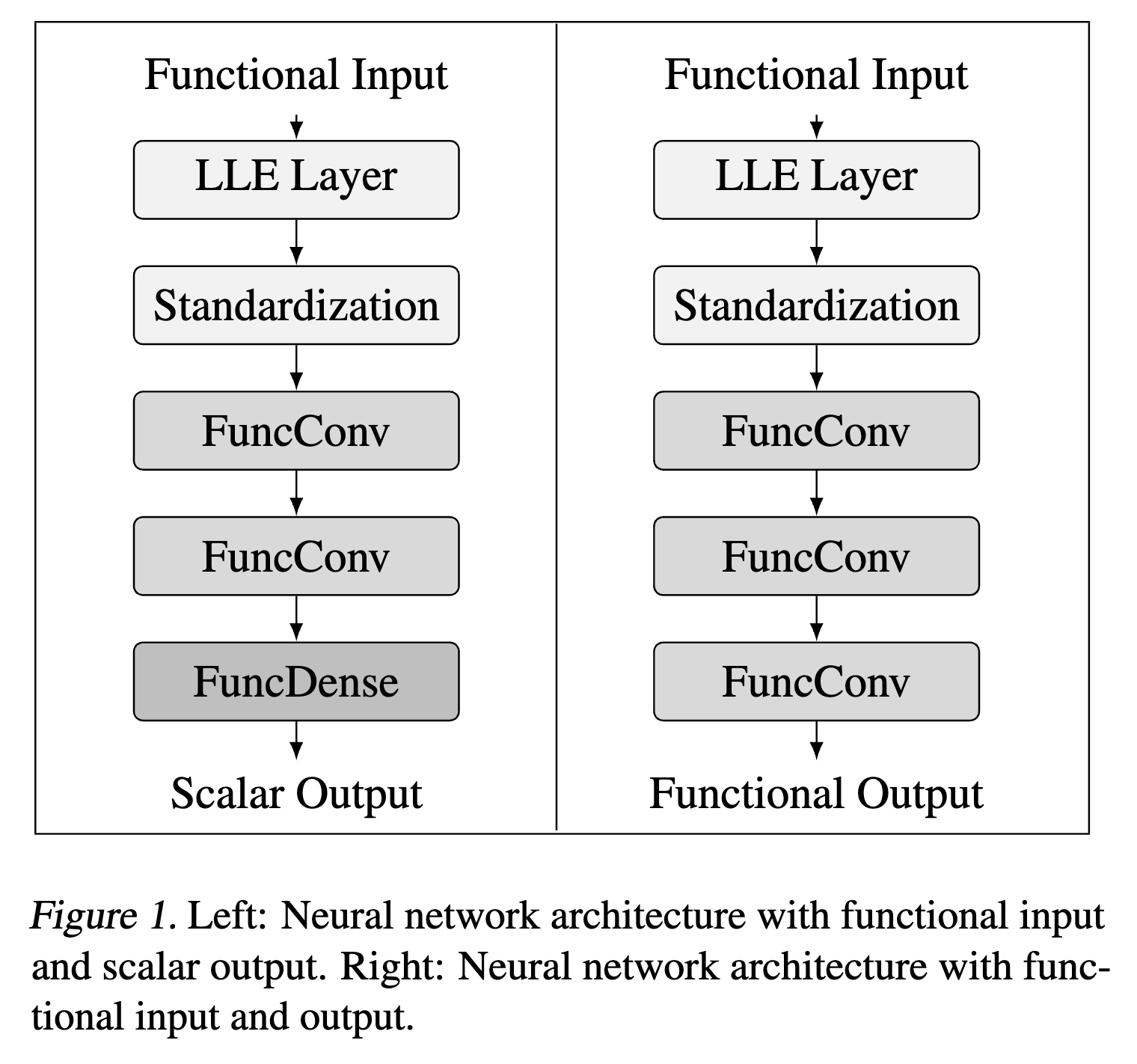
值得注意的是，ICML2023论文FuncConv^[16]将FuncDense改成了卷积神经网络，从而实现了时序维度上的平移不变性Shift Invariant（这个问题在MNIST数据集上就比较容易验证，移动黑白图片中的手写数字后，MLP的准确率容易下降、而CNN则基本维持原有水平），在“函数到函数”的回归任务上也超过了传统基于MLP的FNN方法，这也正是2024年NeurIPS论文FUNNEL^[2]的图2(b)中所提出的与FDA完全并行的方法。

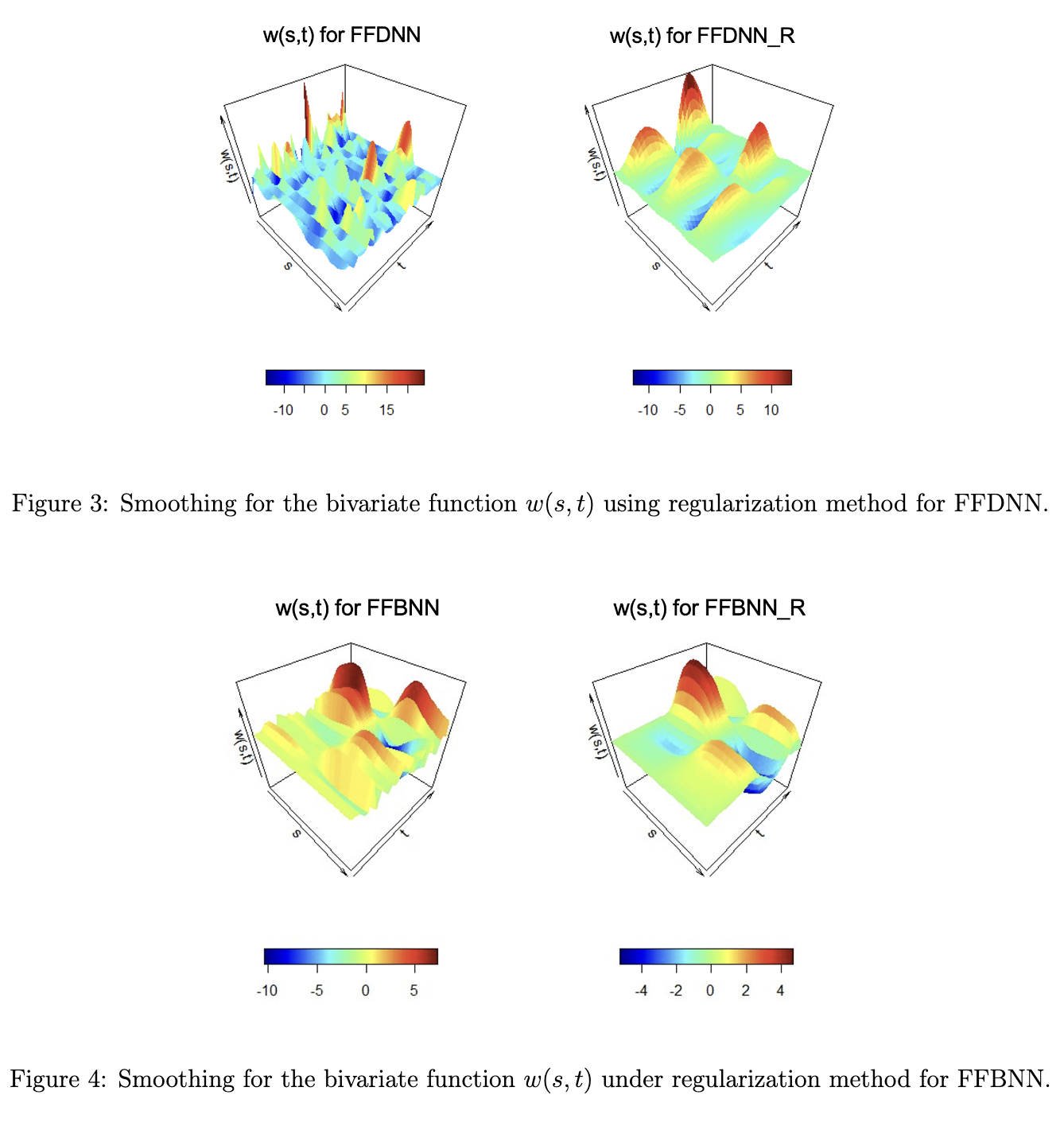
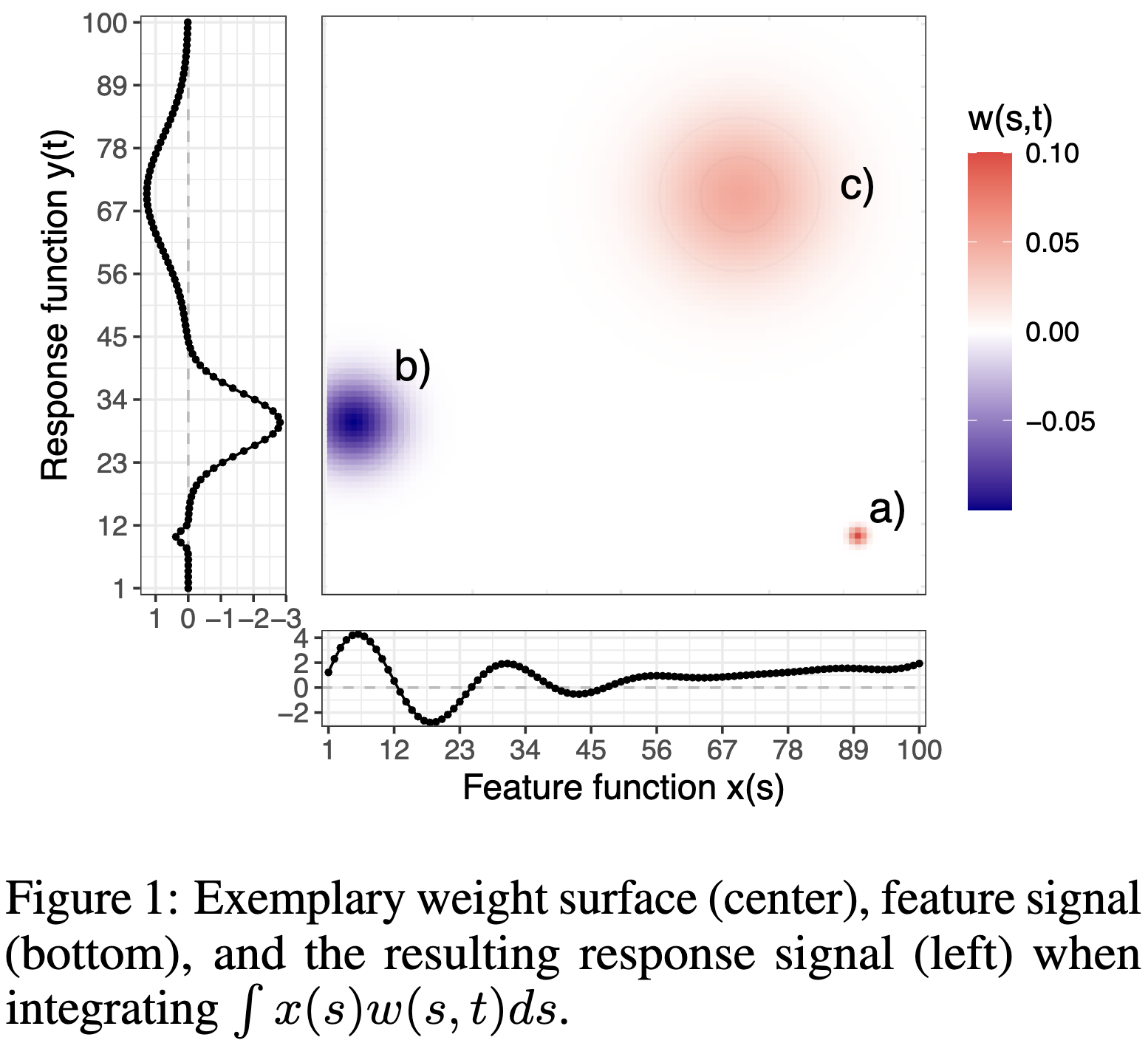
总之，从FBNN到FuncConv，原生支持函数输入、特征提取、函数输出的FNN通过显式地建模每层输入与输出之间的贡献关系映射$W(s, t)$，保证了与FDA类似的可解释性，同时通过基函数展开方法、基函数等间隔采样技巧，实现了与现有深度学习框架的无缝兼容。上图为FBNN原文^[13]中可视化的关系映射$W(s, t)$，其中R代表了对权重平滑度的正则化方法，在不影响精度的情况下，正则化后能够更显著地表达贡献程度。

与Neural CDE的联系 Association with Neural CDE

在之前的笔记中，神经受控微分方程Nerual CDE的设计能够避免Nerual ODE的“初值问题”，也就是为了输入时间序列$\mathrm{X_T}$中新增的一小段$\rm X_{T+\Delta T}$，需要输入完整的当前数据$\rm X=\{X_1, \cdots, X_T, \cdots, X_{T+\Delta T}\}$跑完整个编码器构成的模型，编码得到解码器所需的初始特征$z_0$，然后再从$z_0$开始积分，模型的效率十分感人。

而Neural CDE将输入数据$X$与网络输出特征$f_\theta(z_t)$以系数相乘的形式组合，从而对于$\rm X_{T+\Delta T}$，只需从$z_\mathrm{T}$开始，用新增数据$\rm X’=\{X_{T+1}, \cdots, X_{T+\Delta T}\}$继续积分得到$z’ = \{z_\mathrm{T+1}, \cdots, z_\mathrm{T+\Delta T}\}$即可:

$$
\begin{split}
& z_\mathrm{T} = z_0 + \int_0^\mathrm{T} f_\theta(z_t) \frac{d \mathrm{X}_t}{dt} dt = z_0 + \int_0^\mathrm{T} f_\theta(z_t) d \mathrm{X}_t\\
& \Rightarrow z_\mathrm{T+\Delta T} = z_\mathrm{T} + \int_\mathrm{T}^\mathrm{T+\Delta T} f_\theta(z_t) d \mathrm{X}_t
\end{split}
$$

可以看到，Neural CDE也建立了一个从任意输入函数$\mathrm{X}’$，到输出函数$z’$的“函数到函数”映射关系，而且中间的过程是具有时序因果依赖的，也就是当前时刻$z_\tau$依赖的输入数据应当是$t < \tau$的，不会出现依赖于未来数据的情况。这是经典FDA、FNN所未考虑到的（当然，最简单的方法就是给$w(s, t)$加上一个类似于因果注意力掩码的下三角矩阵）。

但是，这种依赖关系也是非常复杂的，因为当前时刻的$z_\tau$依赖了几乎所有过去的输入函数数据，如果过去有一个$z_{\tau’}$重度依赖了某一个$\mathrm{X}_o$，则后续的$z_\tau$仍需继承这个依赖。反而在FDA、FNN中，输出函数的每一个点的依赖都是相互之间独立的，映射矩阵是输入输出函数的无限维取值点的全连接，也即$W \in L^2\left(\mathcal{U}(c, d) \times \mathcal{U}(a, b)\right)$。那么，同样建模了“函数到函数”的映射关系，这两者之间的优缺点如何合理地互补，这便是一个值得探索的有趣话题。虽然相对当下主流的MLP、RNN、CNN、Transformer、Mamba等神经网络而言更加抽象，但同样可以相信，它们总有一天也会应用在这实际世界上。

参考资料

• [1] Liu Z, Wang Y, Vaidya S, et al. Kan: Kolmogorov-arnold networks[C]. The Thirteenth International Conference on Learning Representations, 2025.
• [2] Rügamer D, Liew B, Altai Z, et al. A Functional Extension of Semi-Structured Networks[J]. Advances in Neural Information Processing Systems, 2024, 37: 129888-129913.
• [3] bsplines.org. Flavors and Types of B-Splines. https://bsplines.org/flavors-and-types-of-b-splines/
• [4] Applied functional data analysis: methods and case studies[M]. New York, NY: Springer New York, 2002.
• [5] Malfait N, Ramsay J O. The historical functional linear model[J]. Canadian Journal of Statistics, 2003, 31(2): 115-128.
• [6] Ramsay J O, Silverman B W. Principal components analysis for functional data[J]. Functional data analysis, 2005: 147-172.
• [7] Wang Q, Wang H, Gupta C, et al. A non-linear function-on-function model for regression with time series data[C]//2020 IEEE International Conference on Big Data (Big Data). IEEE, 2020: 232-239.
• [8] Wang S, Zhang W, Cao G, et al. Functional data analysis using deep neural networks[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2024, 16(4): e70001.
• [9] Thind B, Multani K, Cao J. Deep learning with functional inputs[J]. Journal of Computational and Graphical Statistics, 2023, 32(1): 171-180.
• [10] Yao J, Mueller J, Wang J L. Deep learning for functional data analysis with adaptive basis layers[C]//International conference on machine learning. PMLR, 2021: 11898-11908.
• [11] Rossi F, Conan-Guez B, Fleuret F. Functional data analysis with multi layer perceptrons[C]//Proceedings of the 2002 International Joint Conference on Neural Networks. IJCNN'02 (Cat. No. 02CH37290). IEEE, 2002, 3: 2843-2848.
• [12] Rao A R, Reimherr M. Nonlinear functional modeling using neural networks[J]. Journal of Computational and Graphical Statistics, 2023, 32(4): 1248-1257.
• [13] Rao A R, Reimherr M. Modern non-linear function-on-function regression[J]. Statistics and Computing, 2023, 33(6): 130.
• [14] Aniruddha Rajendra Rao. https://github.com/aniruddharao/FDNN-and-FBNN-JCGS-
• [15] Aniruddha Rajendra Rao. https://github.com/aniruddharao/Function-Neural-network-scalar-response-
• [16] Heinrichs F, Heim M, Weber C. Functional Neural Networks: Shift invariant models for functional data with applications to EEG classification[C]//International Conference on Machine Learning. PMLR, 2023: 12866-12881.
• [17] Florian Heinrichs. https://github.com/FlorianHeinrichs/functional_neural_networks
• [18] David Rügamer. https://github.com/neural-structured-additive-learning/funnel