What I cannot create, I do not understand.
by Richard P. Feynman
本文是关于算子学习Operator Learning的个人笔记
主要是物理信息神经网络PINN、深度算子网络DeepONet的基础知识,以及逆问题求解方法。
前言 Introduction
费曼的这句名言,中文意思是“凡是我无法创造的事物,我就无法理解它”。
这就是我写这些笔记的初衷,如果我不知道这些方法是如何创造的,就无法真正意义上地理解它们。所以,深究方法本身的细节和全貌是不够的,要看它是基于什么既有方法,它的新设计解决了什么问题。虽然,我不可能彻底达到方法原作者的理解程度,总归是比眼里完全只有黑盒,更加逼近这个极限。
另外,这些方法的作者,在研究设计这些全新方法时,大多也经历了类似的过程。无数的方法都是站在巨人的肩膀上,后来者虽然不用重复一遍巨人走过的路,但是仍然要理解巨人创造的过程,从而最终自己实现全新的创造。这就是反过来的说法:“凡是我无法理解的事物,我就无法在它的基础上创造”。
所以这篇笔记写作讲算子学习,读作讲Neural ODE以外的、另一条建模微分方程(ODE和PDE)的技术分支。当然,也不一定真的要从头读到尾,毕竟很多是众所周知的知识。因为下面各种过程不会涉及很深的数学理论,可以根据每章首尾的前后衔接,按需跳读。
物理信息神经网络 Physics-Informed Neural Network
之前的笔记提到过,常微分方程(Ordinary Differential Equation,ODE)是自变量只有一个的微分方程,一般表示的是时间。然而,尤其是在物理领域,自变量往往是多个的(例如一个2D的场随时间的变化,包括$xy$坐标和时间$t$),因此需要引入偏微分方程。例如,描述热传导的傅里叶方程(Fourier’s Equation)的1D、2D形式,其中$u$是一个关于坐标和时间的未知函数,表示的是热量随时间在空间中的传播:
$$
\begin{equation}
\frac{\partial u}{\partial t} = \alpha\frac{\partial^2 u}{\partial x^2}, ~~~~
\frac{\partial u}{\partial t} = \alpha( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2})
\end{equation}
$$
上述方程可以理解为,$u$代表的热量随时间$t$的微分变化,是由$u$在空间坐标上的二阶微分、也就是热量在局部相邻位置的变化方向(一阶微分)的变化大小(二阶微分)引起的。对于此类多个自变量的偏微分方程,之前的Neural ODE[1]就无法建模了。而且,对于一些复杂的物理过程,有时候很难写出关于未知函数$u$的具体表达式,只有形如式子(1)的笼统约束。那么,和Neural ODE一样,我们可以将$u$用一个神经网络来表达。
其中$w$和$b$为神经网络的权重、偏置参数。神经网络的输出$u$就代表了输入$(x, t)^\top$后的函数值
因此,Maziar Raissi等人在2017年提出了物理信息神经网络[2][3](Physics-Informed Neural Network,PINN),该工作最终于2019年发表在计算物理学顶刊Journal of Computational physics[4]。如上图所示,以式子(1)中的1D傅里叶方程为例,一个神经网络$\mathrm{NN}$接受输入的自变量为坐标$x$和时间$t$,它的输出即为$u$,参数为权重$w$(weight)、偏置$b$(bias)。因此,可以看做这个神经网络代替了$u$的具体表达式:
$$
u(x, t)=\mathrm{NN}(x, t | w, b)
$$
如上图所示,对于PINN的训练,其损失函数可以分为以下两个部分:
第一部分是对$u$这个函数的函数值本身进行约束。例如在$t=0$时刻、$x=x_0$上的$u$值,如果已知,就可以当作初始条件(Initial Condition,IC)的真值,剩下的时刻和位置上,如果也有的已知$u$值,就可以当作边界条件(Boundary Condition,BC)的真值,将它们与PINN预测出来的$u$计算差值。
第二部分是对$u$这个函数求各个偏微分方程的值进行约束。同样地,在某个时刻和位置上,如果已知有形如式子(1)、包含$\frac{\partial u}{\partial t}$、$\frac{\partial u}{\partial x}$、$\frac{\partial^2 u}{\partial x^2}$等项的偏微分方程,那么对应计算PINN输出的$u$,相对于输入$x$和$t$的偏导,代入方程的右边得到图中的$g$,然后和左边相减,得到一个差值$R$。因为pytorch等深度学习框架需要计算梯度,因此有
torch.autograd等自动微分API可供调用,这是整个PINN最巧妙的地方,利用神经网络的梯度微分学习机制。
最终,将上述差值送入均方误差函数(Mean Square Error,MSE)后,相加得到最终的损失函数值,当其小于$\epsilon$时,可以认为神经网络的拟合趋于收敛,停止训练。值得注意的是,Neural ODE是需要拟合对ODE计算积分后的真实值,因此使用的是计算对应积分值的$\mathrm{ODESolver(\cdot)}$,详见之前的笔记;而PINN直接计算输出与$u$真实值的差距,同时也需要拟合如式子(1)的偏微分方程,因此使用的是计算对应偏导值的torch.autograd等自动微分API。
如果想要把Neural ODE的任务套用进PINN,则将输入改为只有一个自变量$t$,由于$u=\mathrm{NN}(t)= u_0 + \int \frac{du}{dt} dt$,所以无需任何ODE或PDE约束,只需要包括IC和BC等真实值条件进行约束,退化为了一个普通的神经网络。在无对应ODE或PDE约束的前提下,如果真实值过少,则会导致神经网络过拟合到这几个点上。Neural ODE至少有将神经网络的输出进行积分的关系,也就是$\frac{du}{dt} = \mathrm{NN(u, t)}$, 且$u = u_0 + \int \frac{du}{dt} dt=\mathrm{ODESolver}(\mathrm{NN}, u_0, t_0, t_N)$。
言归正传,在测试阶段,对应的PINN模型输入了$(x, t)^\top$之后,只能输出符合式子(1)等训练时指定的偏微分方程中的函数值$u$。也就是说,一旦训练停止,这个模型就无法适用于新的偏微分方程。例如,改变了初始或边界条件、改变了式子(1)本身,都意味着$u$变了,需要重新训练一个新的PINN模型。
深度算子网络 Deep Operator Network
为了避免重新训练,肯定要想办法在训练时新增额外的输入,使得模型能够泛化到其他偏微分方程上。当然,如果能确定式子(1)本身的大致形式,只是其中的若干参数未知,则可以参见PINN原文第二部分[3],用神经网络拟合未知函数$u$的同时,求解待定参数,具体的方式可以见下一章节。
因此,最重要的是未知函数$u$本身的改变,我们可以将改变这个函数的额外变量输入到网络里。但是,顾名思义,我们无法知道这个函数的具体表达式形式,甚至连大致形式都不知道。因此,对于这个函数的性质,只能通过与之相关的若干数据间接了解。那么,在未知函数$u(y)$本身也要接受$y=(x, t)^\top$等输入的情况下,如何建立从这些额外的数据到未知函数$u$的映射关系呢?
重新定义符号,将间接数据的观测采样点(如时间、位置点)为$\{x_0, \cdots, x_m\}$,每点的第$n$种观测值为函数$u^{(i)}(x_m)$,所有$u^{(i)} \in u$,$u$代表所有的间接数据。定义从间接数据$u$到未知函数的映射为$G$,也就是当前间接数据$u$所描述的未知函数等于$G(u)$。给定输入$y$,这个未知函数的函数值就是$G(u)(y)$。
根据上述的符号定义,我们可以发现,$G$实际上是函数到函数的映射,因为$u^{(i)}(x_m)$是关于观测点$x_m$的函数,$G(u)$是关于所有间接数据$u$的函数。这种映射被称为“算子(Operator)”。一个最直观的例子就是,常微分$\frac{d}{dt}$或偏微分$\frac{\partial}{\partial t}$等算子,可以将给定函数$f$变为另一个函数,也就是$\frac{df}{dt}$或$\frac{\partial f}{\partial t}$。
显然,我们不知道这个算子$G$到底是什么形式的,例如是不是若干个$u^{(i)}$的线性组合得到了未知函数。所以,我们也可以用神经网络来表示这个映射。因此,Chen等人[5]在1995年证明了用神经网络作为算子,同样和普通神经网络一样,满足万能逼近定理(可以拟合任意的算子)。在此基础上,Lu等人[6]在2021年的Nature子刊Nature Machine Intelligence上,发表了深度算子网络DeepONet(Deep Operator Network),提出用更深层的神经网络作为算子。
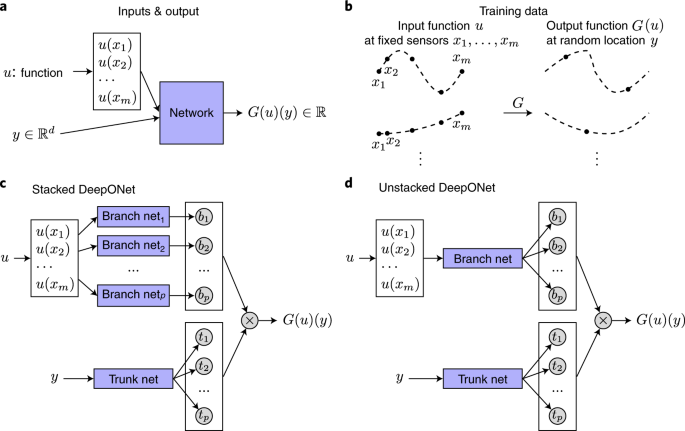
图(b)是训练数据的构成,在若干固定采样点$x_m$上的间接数据函数值$u$,对应任意输入$y$上的函数值
图(c)和(d)是两种DeepONet设计,每个采样点分别还是共同输入“Branch Net”
如上图所示,DeepONet分为两部分:一部分是输入间接数据$u$的“Branch Net”,每个采样点分别输入各自的分支网络,被称为堆叠(Stacked),反之共同输入一个网络,则为非堆叠(Unstacked);另一部分是输入自变量$y$的“Trunk Net”,因为必然只有一条($y$可以是一个向量,代表所有输入,例如包括了空间位置和时间$(x, t)^\top$),所以被称为主干网络。由这两个网络得到的特征$b$和$p$,分别代表$G(u)$和$y$的信息。对应下标的特征相乘求和后,最终得到$G(u)$在自变量为$y$时的函数值$G(u)(y)$。对$G(u)(y)$的约束方式可以是普通的,也可以与PINN类似(称为PI-DeepONet)。
示例 Examples
定义自变量输入只有时间$t$,未知函数为$s(t)$,间接数据为$u(t)$,已知两者的关系满足如下常微分方程:
$$
\begin{equation}
\frac{ds(t)}{dt} = u(t), t\in [0, 1]
\end{equation}
$$
对此进行积分可以得到:
$$
\begin{equation}
s(t) = s(0) + \int_0^t u(t’) dt’
\end{equation}
$$
那么,相应的DeepONet事实上就是在拟合式子(3)这个积分构成的算子,输入函数是$u(t)$,DeepONet输出是$g(t)$。为了不让算子只对一条间接数据时间轨迹过拟合,应当采样多条间接数据的时间轨迹函数$u^{(i)}$;同时,对应的输入自变量$y^{(i)}_j$的真值$G(u^{(i)})(y^{(i)}_j)$也应给出,且满足式子(3)的关系:
$$
\begin{split}
& s(y^{(i)}_j) = G(u^{(i)})(y^{(i)}_j) \\
& = s(0) + \int_0^{y^{(i)}_j} u^{(i)}(t) dt
\end{split}
$$
注意,$i$和$j$之间没有任何关系,有$i$个间接数据函数,每个间接数据的函数$u^{(i)}$可以通过$G$映射到一个未知函数$G(u^{(i)})$,这个未知函数上可以有$j$个任意位置的真值点$G(u^{(i)})(y^{(i)}_j)$。输入$u^{(i)}$的格式,是在该函数上采$x_0, \cdots, x_m$个固定点。因此,对于DeepONet,训练或测试数据由以下$|I| \times |J|$个三元组构成:
$$
\begin{split}
& \left\{ u(x), y, G(u)(y) \right\} \\
& = \left\{ (u^{(i)}(x_0), \cdots, u^{(i)}(x_m))^\top, y^{(i)}_j, G(u^{(i)})(y^{(i)}_j) \right\}_{i \in I, j \in J}
\end{split}
$$
由于式子(3)描述的算子十分通用,对任意的输入函数,都应当满足对应的积分关系。因此,为了充分训练DeepONet,论文原文[6]采用了高斯随机场(Gaussian Random Field,GRF)或切比雪夫多项式(Chebyshev Polynomials),随机生成了若干个函数$u^{(i)}$和对应的真值$s(y^{(i)}_j) = G(u^{(i)})(y^{(i)}_j)$。训练损失函数和PINN是一样的,可以分为两部分,一部分约束输出初值$s(0)$以及其他边界条件,另一部分对输出$s(y^{(i)}_j)$,求$\frac{d}{dt}$用前述真值$G(u^{(i)})(y^{(i)}_j)$约束。
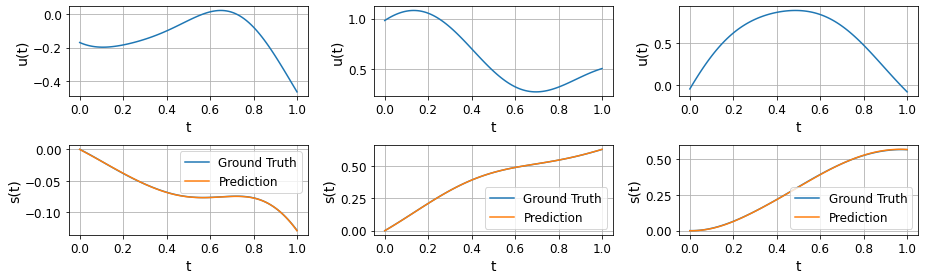
可以看到$s(t)$确实是$u(t)$的积分,反之$u(t)$是$s(t)$的导数,例如$u(t)=0$时,$s(t)$曲线平缓
图片来自GitHub仓库ShuaiGuo16/PI-DeepONet
值得注意的是,除了输入函数$u$的个数$i$外,采样点的数量个数$m$也会影响最终拟合的效果。因此,在实际问题中,应当尽可能多地采集$u^{(i)}$、且尽可能密集地采集每个$u^{(i)}$的$u^{(i)}(x_m)$,从而更好地刻画这些间接数据,生成更准确的位置函数$G(u)$。反过来,对该未知函数的自变量和函数值$(y, G(u)(y))^\top$,实际上只需要少量的采样点,作为PINN损失函数的第一部分。如果已经知道该函数$G(u)(y)$和$u$形如式子(2)的大致关系,则可以纳入到损失函数的第二部分。
逆问题求解方法 Inverse Problem Solving
在上述的示例中可以看出,为了用ODE、PDE约束PINN、DeepONet的网络输出,显然需要已知对应的ODE、PDE的具体形式,例如式子(2)。但是,在很多复杂场景下,ODE、PDE的具体形式未知,需要反过来求解他们,因此称为逆问题(Inverse Problem)。例如,空间位置$x$或时间$t$等一个或多个自变量和网络输出$s$关联,应该是个ODE、PDE,且式子应该和间接数据的函数$u$有关,即多了一层函数$\kappa(\cdot)$,且这个函数本身有待定参数$\tilde{\theta}$。以DeepONet为例,式子(2)改写为:
$$
\frac{ds(t)}{dt} = \kappa(u(t) | \tilde{\theta}), t\in [0, 1]
$$
例如,我们大概知道$\kappa(\cdot)$是一个线性函数,则可以写作(式子(2)就相当于$\omega = 1$, $\beta = 0$):
$$
\begin{equation}
\begin{split}
& \frac{ds(t)}{dt} = \omega \cdot u(t) + \beta, \\
& t\in [0, 1], \tilde{\theta} = \{\omega, \beta\}
\end{split}
\end{equation}
$$
那么,PINN的损失函数第二项就可以改写为(这里函数符号用DeepONet的输出$s(y)=s(x, t)$):
$$
R = \mathcal{L}(s, u, \theta, \tilde{\theta}) - \mathcal{L}(s(x, t), \theta)
$$
其中,第一项使用间接数据函数$u$代入式子(4)右边,计算$s(y)=G(u)(y)$真值,多了待定参数$\tilde{\theta} = \{\omega, \beta\}$,第二项用自动微分API求神经网络输出的$\frac{ds(x, t)}{dt}$。在PyTorch等现代深度学习框架中,可以直接将$\tilde{\theta}$也设置成可学习参数,与PINN、DeepONet的神经网络参数$\theta$一起进行梯度下降优化,在训练收敛后,$\{\omega, \beta\}$的值即为式子(4)的具体形式,在学习了神经网络的同时,求解出了ODE、PDE的近似形式。当然,肯定不仅限于线性函数一种,所以有较高的实用价值。
结语 Conclusions
至此,写好了这篇非常基础的算子学习笔记。实际上,算子学习并没有这么简单,更加本质的数学理论可以继续推导出更精彩的傅里叶神经算子[7](Fourier Neural Operator,FNO)等更强大的神经算子方法,用来求解更复杂的ODE、PDE。这里推荐阅读知乎上熊巍老师的系列专栏,尤其是这一篇。同样地,这也是实践了最开始在前言里提出的“反过来的说法”:“凡是我无法理解的事物,我就无法在它的基础上创造”。让我们继续探索,看懂并创造更多精彩的东西。
参考资料
- [1] Chen R T Q, Rubanova Y, Bettencourt J, et al. Neural ordinary differential equations[J]. Advances in neural information processing systems, 2018, 31.
- [2] Raissi M, Perdikaris P, Karniadakis G E. Physics informed deep learning (part I): Data-driven solutions of nonlinear partial differential equations[J]. arXiv preprint arXiv:1711.10561, 2017.
- [3] Raissi M, Perdikaris P, Karniadakis G E. Physics informed deep learning (part II): Data-driven discovery of nonlinear partial differential equations[J]. arXiv preprint arXiv:1711.10566, 2017.
- [4] Raissi M, Perdikaris P, Karniadakis G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational physics, 2019, 378: 686-707.
- [5] Chen T, Chen H. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems[J]. IEEE transactions on neural networks, 1995, 6(4): 911-917.
- [6] Lu L, Jin P, Pang G, et al. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators[J]. Nature machine intelligence, 2021, 3(3): 218-229.
- [7] Li, Z., Kovachki, N., Azizzadenesheli, K., Liu, B., Bhattacharya, K., Stuart, A., and Anandkumar A., “Fourier Neural Operator for Parametric Partial Differential Equations”[C]//International Conference on Learning Representations, 2021.
感谢阅读!如有意见和建议,欢迎通过首页的联系方式联系作者。
本文参考资料均来源于网络,作者保留相关权利,转载请注明出处。