We are not the stuff that abides,
but patterns that perpetuate themselves.
by Norbert Wiener
本文是关于神经受控微分方程Neural Controlled Differential Equations的学习笔记
主要是Neural CDE对于Neural ODE的反思与改进,以及其与符号回归Symbolic Regression的内在联系。
前言 Introduction
维纳的这句名言,中文意思是:“我们并非静止不变的物品,而是能够自我延续的模式”。
训练结束后,推理阶段的神经网络模型一般会固定其可学习参数$\theta$,这些参数代表了输入数据、中间特征对于特征计算、最终输出的贡献度。因此,我们将其称为权重$W$,当然,还有调整数值总体偏移的偏置$b$。
然而,在复杂多变的实际应用场景中,对于静止不变的神经网络,其泛化性总是有限的。总有那么一个时刻,推理数据与训练数据不再是独立同分布的(i.i.d., independent and identically distributed)。我们需要模型能够根据当下的工况,按照某种模式,调整输入数据的贡献度,从而实现模型的自我延续。
根据特定模式进行有序的反馈调整,能够让自我的稳态保持得更加长久,正是控制理论的核心哲学之一。这便是我引用控制论创始人维纳名言的原因,这也是为什么我要单独讨论神经受控微分方程Neural CDE的原因。这不只是一个简单的Neural ODE分支,而是一套简洁有效的方法论。
初值问题 Initial Value Problem
回顾之前的笔记,无论是显式的状态$y$、还是隐式的特征$z$,常微分方程都意味着自变量只能有一个,那就是时间$t$,而因变量$y$则随着时间$t$变化:
$$
\begin{equation}
\frac{dy}{dt} = f(y_t) ~~\Leftrightarrow~~ dy = f(y_t)dt
\end{equation}
$$
为了得到某个时刻$y_\mathrm{T}$的值,需要对常微分方程进行积分。若方程已知,则有且仅有的额外输入是初值$y_0$:
$$
\begin{equation}
y_\mathrm{T} = y_0 + \int_0^\mathrm{T} dy = y_0 + \int_0^\mathrm{T} f(y_t)dt
\end{equation}
$$
对于Neural ODE[1],为了得到隐式特征$z$的初值$z_0$,需要将已知的时间序列数据$\mathrm{X}$输入到特定的编码器(这里是ODE-RNN)。给定固定的Neural ODE解码器,得到的$z_0$作为唯一的输入,直接决定了之后所有输出的隐式特征$z_\mathrm{T}$。虽然$z_0$也可以通过采样$\mathcal{N}(\mu, \sigma)$多次得到,但是$\mu, \sigma$确定了之后,同样也能确定后续$z_\mathrm{T}$的平均值范围作为输出。

这便是初值问题(IVP,Initial Value Problem):一旦初值决定,结果也就决定了。那么,在时间层面上静止不变的初值输入$z_0$、以及神经网络参数$\theta$,如何应对实时变化、长度$\mathrm{T}$不断增长的时间序列数据$\mathrm{X}$呢?一个最简单的方式,就是当$\mathrm{X}$变长到$\mathrm{T}+\Delta\mathrm{T}$时,重新输入到编码器得到$z_0$、积分得到隐式特征$z_\mathrm{T}$、乃至将$z_\mathrm{T}$映射到显式的预测结果上。
考虑到除了用于解码预测的Neural ODE是一个神经网络,编码器本身也是一个神经网络,为了一个微小的长度增长$\Delta\mathrm{T}$,反复跑完整个pipeline的计算代价十分高昂。显然有一种最简单的方式,将当前时刻$t$的数据$\mathrm{X}_t$也纳入到Neural ODE的神经网络输入中,从而无需对整个$\mathrm{X}$预先编码(对$\mathrm{X}_0$编码得到$z_0$):
$$
\begin{equation}
z_\mathrm{T} = z_0 + \int_0^\mathrm{T} f_\theta(z_t)dt = z_0 + \int_0^\mathrm{T} h_\theta(z_t, \mathrm{X}_t)dt
\end{equation}
$$
显然,这种形式等价于直接使用编码器ODE-RNN,也即当存在$\mathrm{X}_t$的时候,$z_t$与$\mathrm{X}_t$同时输入神经网络$h_\theta$,得到$z_{t+\Delta t}$的更新,反之则和经典Neural ODE一样只有$z_t$作为输入。若对于连续型时间序列,则任意时间$t$都有$\mathrm{X}_t$作为输入,则等价于纯Neural ODE模型。对于离散型时间序列进行插值(例如,B-样条插值),同样能够实现这个效果。
受控微分方程 Controlled Differential Equations
与式子(3)不同的是,Neural CDE论文[2]引入了受控微分方程(CDE,Controlled Differential Equations)的概念,也就是直接将Neural ODE的神经网络$f’_\theta(z_t)$的输出,作为控制变量、也就是时间序列数据$\mathrm{X}_t$的“系数”:
$$
\begin{equation}
dz_t = f’_\theta(z_t)d\mathrm{X}_t
\end{equation}
$$
需要注意的是,由于$dz_t$应当与$z_t$的形状相同,而$\mathrm{X}_t \in \mathbb{R}^\mathrm{D’}$可能与$z_t \in \mathbb{R}^\mathrm{D}$形状不同,也即隐式特征的维度与显式时间序列数据的维度不同。因此,神经网络$f’_\theta(z_t)$的输出形状不再是与$z_t$一样的向量,而是形状为$\mathrm{D} \times\mathrm{D’}$的线性映射矩阵。
$$
\begin{equation}
z_\mathrm{T} = z_0 + \int_0^\mathrm{T} dz_t = z_0 + \int_0^\mathrm{T} f’_\theta(z_t) d\mathrm{X}_t
\end{equation}
$$
其中,$d\mathrm{X}_t$为时间序列数据$\mathrm{X}$的瞬时变化量(不是导数);则$\frac{d\mathrm{X}_t}{dt}$为时间序列数据的瞬时变化率,也就是一阶导数。那么显然,可以通过$\frac{d\mathrm{X}_t}{dt}$,使得式子(5)的积分也能够用以$t$为变量的常微分方程$g_{\theta, X}(z_t)$表示:
$$
\begin{equation}
\int_0^\mathrm{T} f’_\theta(z_t)\frac{d\mathrm{X}_t}{dt}dt = \int_0^\mathrm{T} g_{\theta, X}(z_t)dt
\end{equation}
$$
Neural CDE证明了式子(5)能够表示任意式子(3),但反过来存在式子(3)无法表示的式子(5),证明过程非常复杂,但是B站上的视频提供了一个形象的例子。定义$y_t$(论文及图片中为$y_s$)为一维的显式状态,Neural CDE的神经网络$f’_\theta(y_t)$输出则从矩阵变成了形状为$\mathrm{D} \times 1$的向量。如果给时间序列数据加一个常量维度1,假设$f’_\theta(y_t)$学到了需要一直输出one-hot的向量,则该积分结果可以表示为初值加上时间序列长度:
$$
\begin{equation}
y_\mathrm{T} = y_0 + \int_0^\mathrm{T} dt = y_0 + \mathrm{T}
\end{equation}
$$

反之,如果$f’_\theta(y_t)$学到的不是一直输出one-hot向量,则是对输入数据——也就是常量维度1、时间序列数据维度$\frac{d\mathrm{X}_t}{dt}$——的加权权重,随着输入$y_t$的变化而变化的。其中常量维度1乘上对应权重向量后,可以看做偏置,即:
$$
\begin{equation}
\frac{dy}{dt} = f’_\theta(z_t)[1, \frac{d\mathrm{X}_t}{dt}]^\top = W_t^\top \frac{d\mathrm{X}_t}{dt} + b_t
\end{equation}
$$
但是,在推理过程中,式子(3)Neural ODE的输入层参数$\{W_1, b_1\} \in \theta$是固定不变的,不随着输入$y_t$的变化而变化,这等价于在Neural CDE中,$f’_\theta(y_t)$输出的$\{W_t, b_t\}$一直是定值$\{W_1, b_1\} $。因此,Neural CDE具有更强大的表达能力。
反馈控制参数 Feedback-Controlled Parameters
然而,正是这个形象的例子,启发了笔者对Neural CDE的进一步思考:真的只有时间序列数据$\mathrm{X}_t$是“控制变量”吗?
我们似乎忽略了一个事实:什么能动态改变作用在$\mathrm{X}_t$上的权重$\{W_t, b_t\}$呢?是式子(5)的神经网络$f’_\theta(y_t)$。在式子(3)的Neural ODE中,上一个时刻的积分结果$y_t$单纯只是输入,无法改变作用在输入上的模型参数$\{W_1, b_1\}$。但是在Neural CDE中,$y_t$能够通过$f’_\theta(y_t)$改变神经网络的输出,也正是作用在输入上的参数$\{W_t, b_t\}$。
而这个$y_t$,正是由再上一个时刻$t-1$的积分结果$y_{t-1}$得到的$\{W_{t-1}, b_{t-1}\}$、以及输入的时间序列数据$\mathrm{X}_{t-1}$共同作用得到的。这是一个不断通过历史结果$y_t$的实时反馈,控制、调整下一个时刻作用在输入$\mathrm{X}_t$的权重,进行“闭环控制”的过程。这是自动化控制中最基本的理论模型。反过来,Neural ODE虽然也输入$y_t$,但无法控制作用在输入$\mathrm{X}_t$的权重。

图片来自Elprocus.com
如上图所示,甚至在闭环控制模型中,反馈调整的方式就是通过对输入乘以权重(乘号$\otimes$)实现的;生成这一权重的输入,也正是“Output”历史结果$y_t$。因此,笔者个人认为,Neural CDE[1]原文第二页底部,对于受控微分方程“Controlled Differential Equations”的注解“Not to be confused with the similarly-named but separate field of control theory”其实并不准确,这并不仅仅是名字像,而是在内在方法论上的共通,简洁而有效。
符号回归 Symbolic Regression
显然,式子(8)中的反馈控制参数$\{W_t, b_t\}$和输入$\mathrm{X}_t$的关系是一个线性多项式,既没有任何的非线性项、也没有函数的嵌套关系。所以,Neural CDE描述复杂现实场景的能力其实仍然有限。当然,神经网络$f’_\theta(y_t)$本身是一个非线性函数,应当能够间接地学习到每个时刻如何精确地调整$\{W_t, b_t\}$,但单纯调整线性权重明显是不够的。
那么,怎样能学习到更高阶的函数关系呢?符号回归(Symbolic Regression)显然是一个值得考虑的选项,顺带还有一个诱人的赠品,就是拟合到的模型本身就是一个可解释的、显式的函数表达式,而不是神经网络参数这样的黑箱。
这里介绍两个比较热门的符号回归流派:基于预定义函数库的SINDy[4](Sparse Identification of Nonlinear Dynamical Systems)、以及近期提出并大火的基于可学习激活函数KAN[5](Kolmogorov-Arnold Networks)。
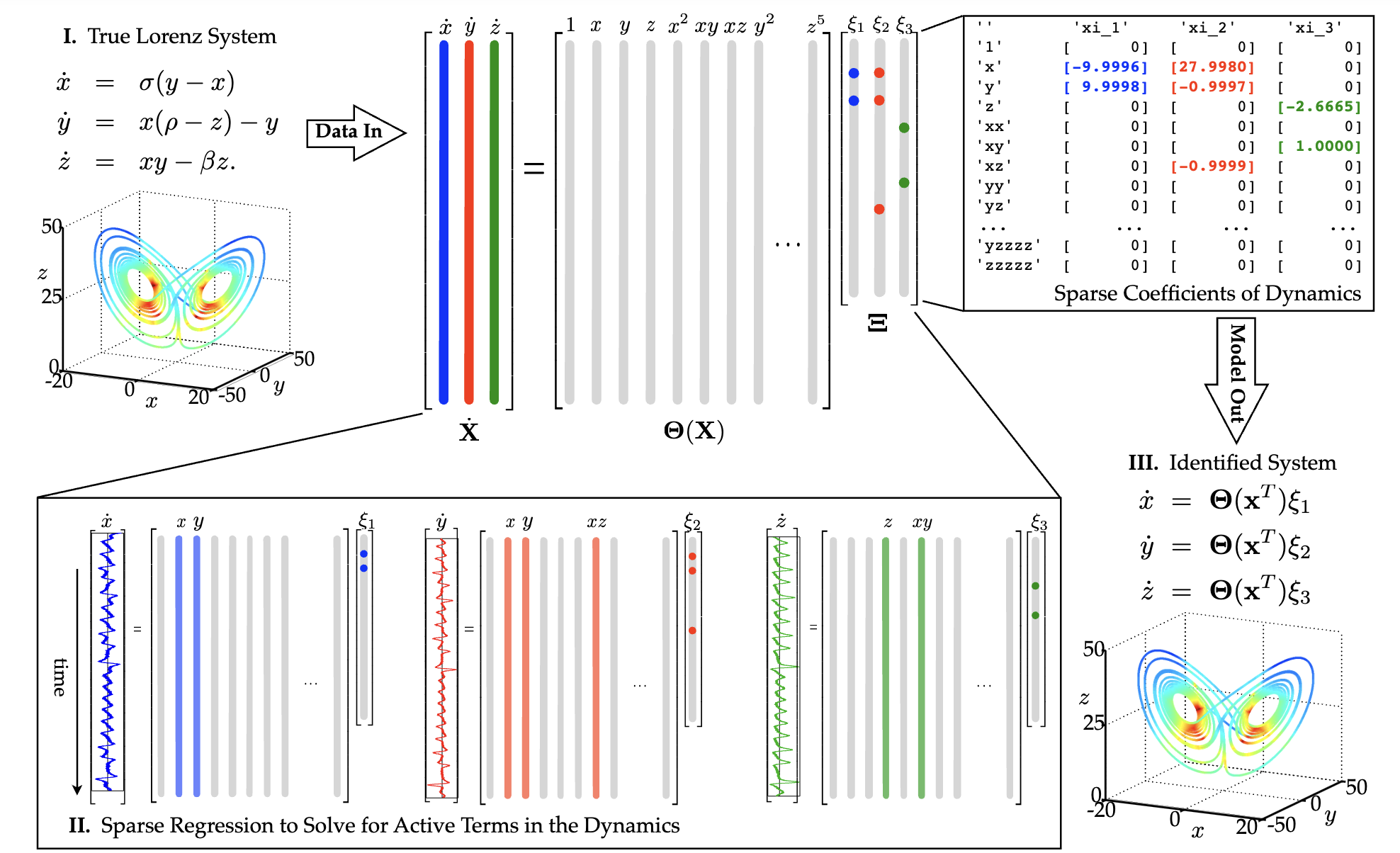
SINDy需要预先定义一系列候选函数算子$\Theta$,一般包括多次项组合(例如,$x, y, x^2, y^2, xy, x^2y, xy^2 \cdots$)、三角函数、对数函数、自然指数函数等常见函数。将输入数据的各个维度代入这些函数,得到一系列函数值。目标是找到一个稀疏的向量$\Xi$,用尽可能少的函数,正确拟合出对应输入的真值。
对于非深度学习的原始版本SINDy,拟合是通过多元回归等数值方法进行的,需要约束$\Xi$的稀疏性。对于基于深度学习的SINDy,可以将$\Xi$作为神经网络参数,进行梯度下降优化,例如结合Neural ODE得到Neural SINDy[6]、多层嵌套的Nested-SINDy等[7]。学到$\mathbf{\Theta}(\mathbf{X})\Xi$即为多项式相加表达式,无法表示、或者只能表示预设的[7]函数嵌套高阶关系。
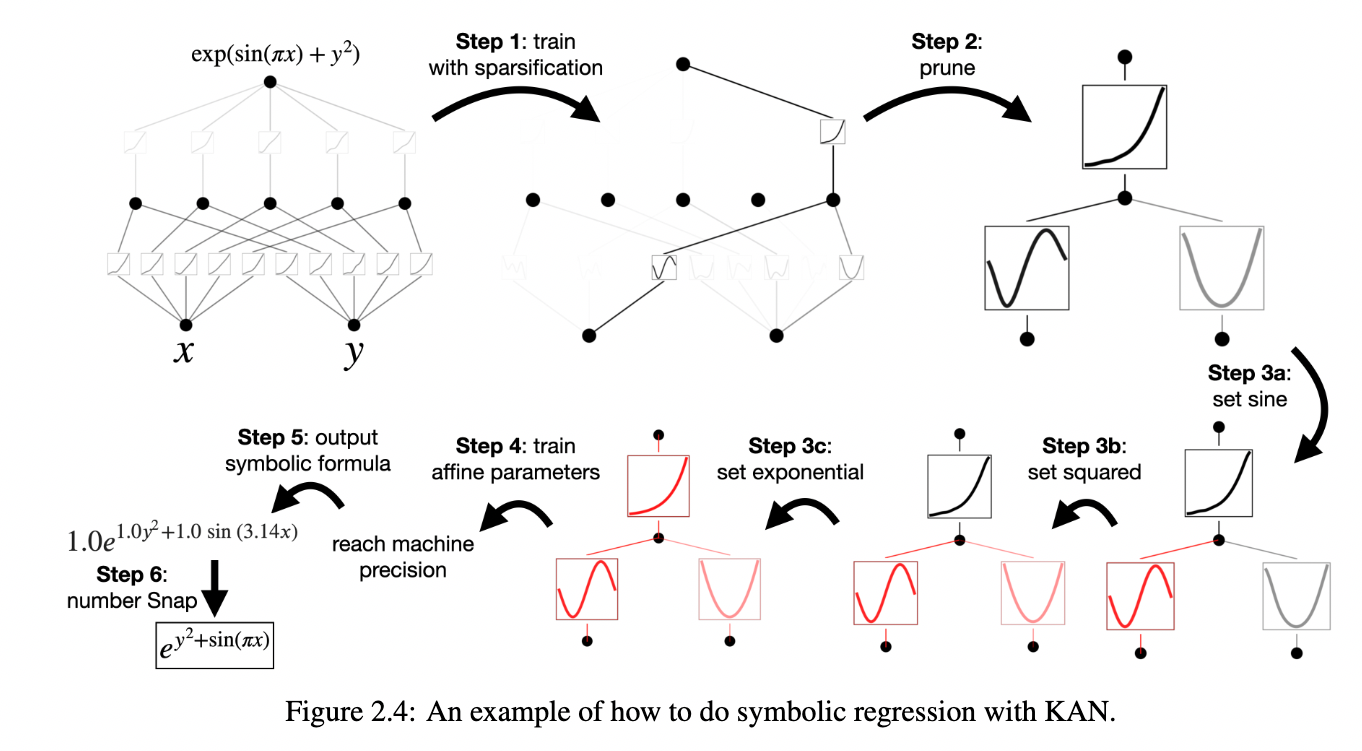
图片来自论文原文[5]
不同于可学习连接权重的传统神经网络,KAN将所有连接权重设置为1,同时将之前固定不可学习的激活函数转变为可学习的。学习目标是通过学习激活函数的B-样条曲线,得到若干个任意形状激活函数的嵌套组合,同时逐步删去无激活函数的权重,从而回归出对应输入的真值。同时,在学习结束后通过对曲线的特定解析方法,可以得到这些曲线组合后的显式表达式,这种解析方法支持生成函数的嵌套关系,具有更高的可解释性和实用价值。
值得注意的是,这些符号回归方法的表达式参数,在训练结束之后仍然是固定的、与输入数据无关的。近期工作DeepOKAN[8]从DeepONet[9]的角度实现了这个思路。所以,这个方向上还有更多的可能性,等待着大家的不断探索。
参考资料
- [1] Chen R T Q, Rubanova Y, Bettencourt J, et al. Neural ordinary differential equations[J]. Advances in neural information processing systems, 2018, 31.
- [2] Kidger P, Morrill J, Foster J, et al. Neural controlled differential equations for irregular time series[J]. Advances in Neural Information Processing Systems, 2020, 33: 6696-6707.
- [3] yyxzhj. Neural ODE, CDE... 神经微分方程大家族. https://www.bilibili.com/video/BV1F44y1X7o6
- [4] Brunton S L, Proctor J L, Kutz J N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems[J]. Proceedings of the national academy of sciences, 2016, 113(15): 3932-3937.
- [5] Liu Z, Wang Y, Vaidya S, et al. Kan: Kolmogorov-arnold networks[J]. arXiv preprint arXiv:2404.19756, 2024.
- [6] Lee K, Trask N, Stinis P. Structure-preserving sparse identification of nonlinear dynamics for data-driven modeling[C]//Mathematical and Scientific Machine Learning. PMLR, 2022: 65-80.
- [7] Fiorini C, Flint C, Fostier L, et al. Generalizing the SINDy approach with nested neural networks[J]. arXiv preprint arXiv:2404.15742, 2024.
- [8] Abueidda D W, Pantidis P, Mobasher M E. DeepOKAN: Deep Operator Network Based on Kolmogorov Arnold Networks for Mechanics Problems[J]. arXiv preprint arXiv:2405.19143, 2024.
- [9] Lu L, Jin P, Pang G, et al. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators[J]. Nature machine intelligence, 2021, 3(3): 218-229.