Finite systems of deterministic ordinary nonlinear differential equations
may be designed to represent
forced dissipative hydrodynamic flow.
in Deterministic Nonperiodic Flow, Edward Lorenz
本文是关于神经流模型Neural Flows的学习笔记
主要是其作为Neural ODE的全新迭代,以及可逆残差网络Invertible Residual Networks和相关补充知识
前言 Introduction
在发现“蝴蝶效应”的著名论文《确定性的非周期流动》[1]中,混沌理论之父爱德华·洛伦兹写下了上面这段话:“可以设计由确定性非线性常微分方程构成的有限系统,来表示受外力耗散流体的流动”。
这个世界终究是物理的。在扩散模型Diffusion被成功引入到图像生成任务后,郎之万动力学Langevin Dynamics[2]、可逆过程Reverse Process[3]、归一化流Normalizing Flow[4],各种物理模型被先后引入进来。最终,各个角度被统一成随机微分方程Stochastic Differential Equation[5],并可以被确定的常微分方程Ordinary Differential Equation表示[6]。
微分方程不仅是教材上的几个章节,它是解析这个物理世界的工具之一。但也正因为是相对统一的工具,如果用更符合物理规律的理论来建模,就有机会更好地拟合这个世界的底层细节。所以,出现比Neural ODE[7]更加迭代的全新模型是必然的,只是应当选取哪一种物理模型而已。本次笔记要介绍的就是神经流模型Neural Flows[8]。
常微分方程的可逆性 Invertibility of ODE
在物理层面上,流体的流动是基于向量映射关系的,也就是当前时刻$t$的某个位置$x_t$,到下一个时刻$t+\Delta t$应当流动到位置$x_{t+\Delta t}$,可以构成一个向量$\vec{x_t}$;对于所有位置$\mathrm{X}_t$,则有向量场$\vec{\mathrm{X}_t}$。
显然地,给定一个初始位置$x_0$,通过在$\vec{\mathrm{X}_t}$中无数次的流动过程,到第$\mathrm{T}$个时刻时,有且只有一个最终位置$x_\mathrm{T}$。也就是说,从起点到终点同样需要符合映射关系,否则就会出现同一个起点vs多个终点、或者一个终点vs多个起点的问题。
为了描述这种性质,我们需要将映射定义为可逆映射,也就是给定终点,同样要能够通过相反方向得到终点。而这种性质,恰好是常微分方程ODE能够满足的:
$$
\begin{equation}
x_\mathrm{T} = x_0 + \int_0^\mathrm{T} \frac{dx}{dt} dt
\end{equation}
$$
$$
\begin{equation}
x_0 = x_\mathrm{T} - \int_0^\mathrm{T} \frac{dx}{dt} dt = x_\mathrm{T} + \int_\mathrm{T}^0 \frac{dx}{dt} dt
\end{equation}
$$
在式子(1)中,可以看到正向积分$\int_0^\mathrm{T} \frac{dx}{dt} dt$;而式子(2)中,可以看到反向积分$\int_\mathrm{T}^0 \frac{dx}{dt} dt$。也就是说,常微分方程$\frac{dx}{dt}=f(x)$可以处理前一个积分结果$x_t$,或者后一个积分结果$x_{t+\Delta t}$,输出变化量$f(x)$:
$$
\begin{align}
& x_{t+\Delta t} = x_t + f(x_t) \Delta t \\
& x_{t} = x_{t+\Delta t} - f(x_{t+\Delta t}) \Delta t \\
\end{align}
$$
神经流模型 Neural Flows
然而,回顾之前的笔记,计算常微分方程的积分是有代价的,那便是数值求解器$\mathrm{ODESolver}$。从$0$到$\mathrm{T}$的过程越长,计算$x_\mathrm{T}$花费的时间和存储就越高,即使是各种新的数值求解器也避免不了这个问题,只能尽量用可变步长等方式缓解。

只关心起始点$x_0$和时间$\mathrm{T}$。图片来自论文原文[8]
那么,是否能够在去掉$\mathrm{ODESolver}$的前提下,保留一个能够满足式子(1)和(2)的$x_0$与$x_\mathrm{T}$双向、可逆映射的神经网络呢?这个神经网络只需要输入初值是$x_0$、终点时间是$\mathrm{T}$,就能直接输出$x_\mathrm{T}$,也就是:
$$
\begin{equation}
\forall x_0, \mathrm{T},~~~ x_\mathrm{T} = F(\mathrm{T}, x_0)
\end{equation}
$$
从物理的角度看,这个条件就是流体的流动过程,所以为了和Neural ODE区分,称为神经流模型Neural Flow。但是,普通的神经网络可以满足这个性质吗?反例是,一个神经网络可能会对不同的$(x_0, \mathrm{T})$,输出同样的$x_\mathrm{T}$(联想一下,分类问题是不是就是这样,需要把不同数据输出为同一个类),这就与式子(1)和(2)矛盾了。
可逆残差网络 Invertible Residual Networks
Neural Flow用到了可逆残差网络,是Neural ODE作者陈天琦等人在ICML 2019上发表的工作[9],与之前的可逆神经网络[10]完全不同的是,这篇文章提出了一个极其简洁的约束方式,使得神经网络能够满足双向、可逆的性质。
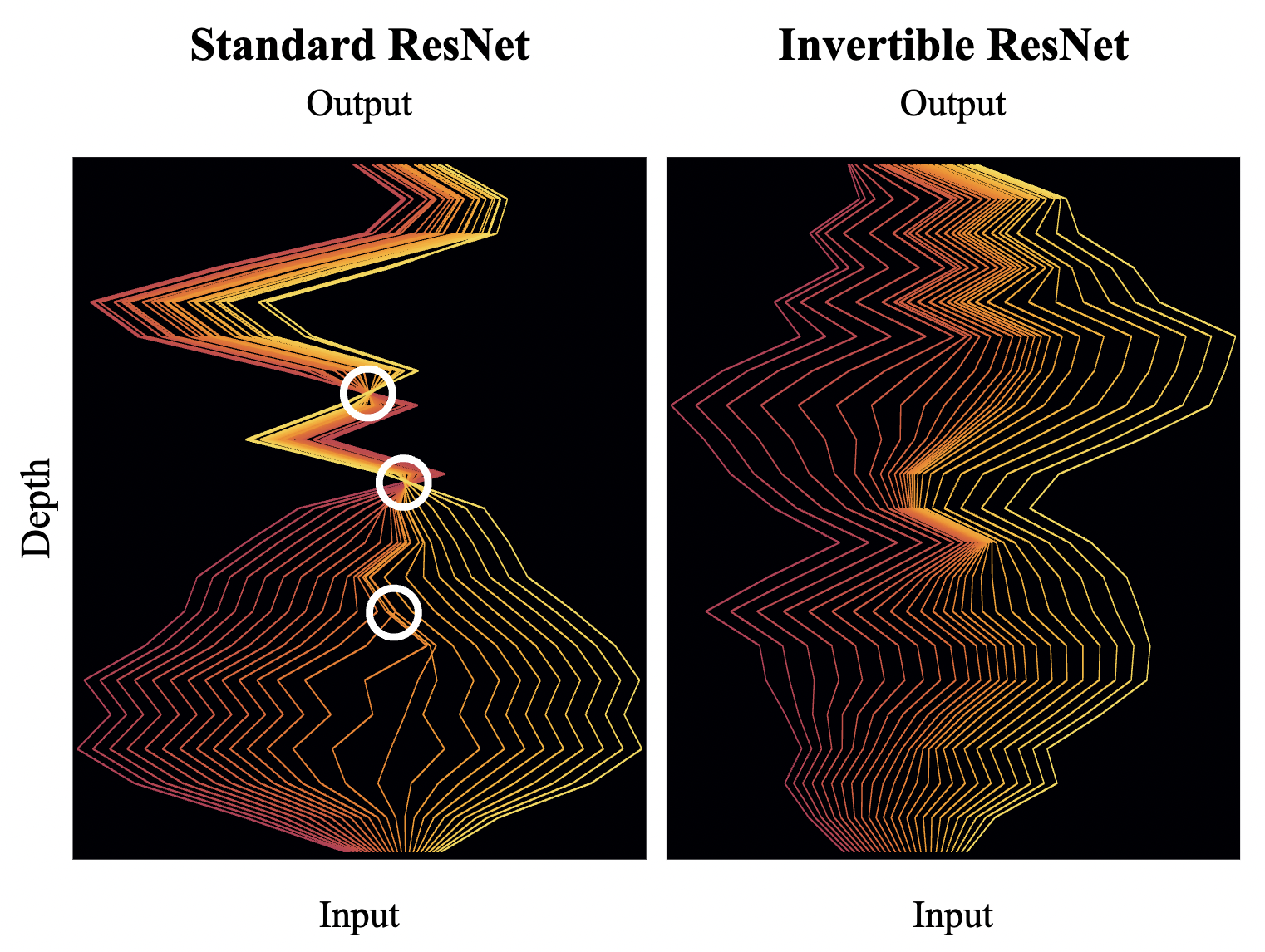
不断普通ResNet的过程中存在若干交叉,上2个交叉甚至是整体的坍塌,导致无法从Output逆向
图片来自论文原文[9]
首先,将一个普通的残差模块描述为式子(6)。同时,可以通过定义步长$h \rightarrow 0$,将其重组为一个常微分方程ODE:
$$
\begin{align}
& x_{t+1} = x_t + g_{\theta_t}(x_t) \\
\Rightarrow & x_{t+1} - x_t = g_{\theta_t}(x_t)\nonumber \\
\Rightarrow & x_{t+h} - x_t = hf_{\theta_t}(x_t) \\
\Rightarrow & \lim_{h\rightarrow 0} \frac{x_{t+h} - x_t}{h} = f_{\theta_t}(x_t)\nonumber \\
\Rightarrow & \frac{dx_t}{dt} = f_{\theta_t}(x_t) \\
\end{align}
$$
那么,对于式子(7),同样可以认为有逆向过程:
$$
\begin{equation}
x_t = x_{t+h} - hf_{\theta_t}(x_t)
\end{equation}
$$
但是,仔细比较残差模块的式子(7)和常微分方程的式子(4)可以发现,既然$h = \Delta t \rightarrow 0$,那么唯一的区别就是$f(x)$的输入不一样,式子(4)是$x_{t+\Delta t}$,而式子(7)是$x_{t}$。也就是说,残差模块$f_{\theta_t}(x)$无法将$x_{t+h}$作为输入进行逆向计算,并不是一个真正的ODE。从另一个角度看,这也是一个经典的“先有鸡、先有蛋”悖论,既然都要求解$x_t$,是个未知量,还得通过$x_t$才能得到$f_{\theta_t}(x_t)$。很显然,这是自相矛盾的,也不符合ODE的可逆性质。
利普希茨连续性 Lipschitz Continuity
按照ODE的结构,重写残差模块的逆向过程:对于$h\rightarrow 0$,给定已知的$x_{t+h}$,$f_{\theta_t}$需要支持输入$x_{t+h}$,得到前一个$x_t$:
$$
\begin{equation}
x_t = x_{t+h} - hf_{\theta_{t+h}}(x_{t+h}) \nonumber
\end{equation}
$$
但是,宏观上ResNet的残差模块只支持离散的步长$h = 1, f_{\theta_{t+h}}=f_{\theta_{t}}=g_{\theta_{t}}$的情况,所以ODE的结构无法直接照搬。为了在离散步长$h=1$条件下,使得固定残差模块$f_{\theta_{t}}$满足连续步长的性质,将式子(10)改写为一个反复迭代的过程:
$$
\begin{equation}
\forall n \in \mathbb{N}, x_t^0=x_{t+1} \Rightarrow x_t^{n+1} = x_{t+1} - g_{\theta_t}(x_t^n)
\end{equation}
$$
显然,我们希望这个逆向的过程能够收敛到唯一的$x_t$上,所以需要满足$\Vert x_t^{n+1} - x_t^{n}\Vert \rightarrow 0$:
$$
\begin{equation}
\lim_{n \rightarrow \infty} x_t^n = x_t \Rightarrow \forall n\rightarrow \infty,~ \Vert x_t^{n+1} - x_t^n\Vert \rightarrow 0
\end{equation}
$$
这里主要参考苏剑林的推导过程[11],此处省略$t$和$\theta_t$,因为除了上标$n$以外,所有的下标都不变。可以代入式子(10),改写为函数$g(x)$的绝对差值:
$$
\begin{equation}
\Vert x_{n+1} - x_n \Vert = \Vert g(x_n) - g(x_{n-1})\Vert
\end{equation}
$$
那么两个函数的绝对差值是否有一个使其趋近于0的上界呢?这里就可以用到函数的利普希茨常数(Lipschitz Constant):函数任意两点斜率绝对值的上确界(最大值),记作$\mathrm{Lip}(g)$:
$$
\begin{align}
& \mathrm{Lip(g)} = \sup_{x_1 \neq x_2} \frac{\Vert g(x_1) - g(x_2)\Vert}{\Vert x_1 - x_2 \Vert} \nonumber \\
& \Rightarrow \frac{\Vert g(x_1) - g(x_2)\Vert}{\Vert x_1 - x_2 \Vert} \leq \mathrm{Lip(g)} \nonumber \\
& \Rightarrow \Vert g(x_1) - g(x_2)\Vert \leq \mathrm{Lip(g)} \Vert x_1 - x_2 \Vert
\end{align}
$$
例如,ReLU函数的$\mathrm{Lip}(g)=1$;抛物线函数$x^2$的一阶导为$2x \in (-\infty, +\infty)$,则$\mathrm{Lip}(g) = \infty$。像ReLU这样,存在一个常数$\mathrm{k}_0$,使得函数$g$的利普希茨常数$\mathrm{Lip}(g) \leq \mathrm{k}_0$,那么称这个函数满足利普希茨连续性 (Lipschitz Continuity):
$$
\begin{equation}
\mathrm{Lip(g)} \leq \mathrm{k}_0 \Rightarrow \Vert g(x_1) - g(x_2)\Vert \leq \mathrm{k}_0 \Vert x_1 - x_2 \Vert
\end{equation}
$$


还能进一步推导出,利普希茨常数有界的意义:在任意两点之间,函数值变化不会过于剧烈。视频截图来自B站[12]
如上图所示,利普希茨连续性直观地保证了任意两点之间,函数的变化是有上下界的,从而使得两个函数的绝对差值是有上界的。因此,将式子(13)代入式子(12),我们可以得到推导过程:
$$
\begin{split}
\Vert x_{n+1} - x_n \Vert & = \Vert g(x_n) - g(x_{n-1})\Vert \\
& \leq \mathrm{Lip(g)} \Vert x_n - x_{n-1} \Vert \\
& = \mathrm{Lip(g)} \Vert g(x_{n-1}) - g(x_{n-2})\Vert \\
& \leq \mathrm{Lip(g)}^2 \Vert x_{n-1} - x_{n-2} \Vert \\
& \cdots \\
& \leq \mathrm{Lip(g)}^n \Vert x_1 - x_0 \Vert
\end{split}
$$
显然,当满足式子(11)的$\Vert x_{n+1} - x_{n}\Vert \rightarrow 0$时,$\mathrm{Lip(g)} < 1$,否则将趋近于1或者$\infty$。这个条件正是要求函数$g$、也即残差模块神经网络,满足式子(14)的利普希茨连续性。直观上看,这就是要求在式子(10)这种逆向过程中,函数的输出不能剧烈跳变,要逐步迭代收敛到逆向的目标$x_t$上。
但是,相邻两点$\Vert x_{n+1} - x_{n}\Vert \rightarrow 0$无法保证绝对收敛,一个反例就是自然对数函数$\ln(x)$,虽然相邻两点变化幅度不大,但它在$n\rightarrow \infty$时是发散的。因此,需要保证任意两点间的$\Vert x_{n+m} - x_{n}\Vert \rightarrow 0$:
$$
\begin{split}
\Vert x_{n+m} - x_{n}\Vert & \leq\Vert x_{n+m} - x_{n+m-1}\Vert+\cdots \\
& +\Vert x_{n+2} - x_{n+1}\Vert+\Vert x_{n+1} - x_{n}\Vert\\
&\leq \left(\mathrm{Lip}(g)^{n+m-1}+\cdots+\mathrm{Lip}(g)^{n}\right)\Vert x_{1} - x_{0}\Vert\\
& = \frac{1 - \mathrm{Lip}(g)^m}{1 - \mathrm{Lip}(g)}\cdot\mathrm{Lip}(g)^{n}\Vert x_{1} - x_{0}\Vert\\
& \leq \frac{\mathrm{Lip}(g)^n}{1 - \mathrm{Lip}(g)}\Vert x_{1} - x_{0}\Vert
\end{split}
$$
同样地,为了$\Vert x_{n+m} - x_{n}\Vert \rightarrow 0$,应当有$\mathrm{Lip(g)} < 1$,否则无解($\mathrm{Lip(g)} = 1$)或趋近于$\infty$。当$m \rightarrow \infty$时:
$$
\Vert x_\infty - x_{n}\Vert \leq \frac{\mathrm{Lip}(g)^n}{1 - \mathrm{Lip}(g)}\Vert x_{1} - x_{0}\Vert
$$
这个不等式就是著名的巴拿赫不动点定理(Banach Fixed Point Theorem),又名压缩映射定理。其中,不动点指的是$x_\infty$,压缩指的是函数$g$,映射指的是距离度量方式$\Vert \cdot \Vert$。把之前省略的下标再放回来,$x_\infty$就是逆向的目标$x_t^\infty=x_t$。
谱范数 Spectral Norm
那么,既然知道了需要满足所有残差模块$g$的利普希茨常数$\mathrm{Lip}(g) < 1$,如何实现这个约束呢?首先,我们知道ReLU、Sigmoid等常用的激活函数已经满足了这个约束。那么,实际上就是要给神经网络的权重$W$的利普希茨常数$\mathrm{Lip}(W)$进行约束,可以将式子(13)改写为:
$$
\Vert W(x_1 - x_2) \Vert \leq \mathrm{Lip}(W)\Vert x_1 - x_2 \Vert
$$
我们可以尝试把$W$从范数中提取出来。神经网络的权重通常是一个矩阵$W \in \mathbb{R}^{\mathrm{D}\times \mathrm{D’}}$,而求矩阵的范数一般采用谱范数(Spectral Norm)$\Vert W \Vert_2$:
$$
\begin{split}
& \Vert W(x_1 - x_2) \Vert \leq \Vert W \Vert_2 \cdot \Vert x_1 - x_2 \Vert, \mathrm{Lip}(W) < 1 \\
& \Rightarrow \Vert W \Vert_2 \leq 1
\end{split}
$$
参考苏剑林的推导过程[13],谱范数$\Vert W \Vert_2$的定义是$W^\top W$的最大特征根的平方根,其中$x$为单位向量:
$$
\Vert W\Vert_2^2 = \max_{x\neq 0}\frac{x^{\top}W^{\top} Wx}{x^{\top} x} = \max_{\Vert x\Vert=1}x^{\top}W^{\top} Wx
$$
将$W^\top W$对角化为$\text{diag}(\lambda_1,\dots,\lambda_n)$,也即$W^{\top} W=U^{\top}\text{diag}(\lambda_1,\dots,\lambda_n)U$,$U$是正交矩阵,任意$\lambda$非负:
$$
\begin{aligned}
\Vert W\Vert_2^2 =& \max_{\Vert x\Vert=1}x^{\top}\text{diag}(\lambda_1,\dots,\lambda_n) x \\
=& \max_{\Vert x\Vert=1} \lambda_1 x_1^2 + \dots + \lambda_n x_n^2\\
\leq & \max\{\lambda_1,\dots,\lambda_n\} (x_1^2 + \dots + x_n^2) \\
=&\max\{\lambda_1,\dots,\lambda_n\}
\end{aligned}
$$
在求得谱范数$\Vert W\Vert_2$后,只需要对所有的残差模块权重用$\Vert W\Vert_2$归一化,然后再乘上$c \in (0, 1)$即可:
$$
\begin{equation}
W^* = c \cdot \frac{W}{\Vert W\Vert_2}
\end{equation}
$$
利普希茨角度的可逆性 Invertibility by Lipschitz
对于Neural ODE,由于常微分方程$\frac{dx}{dt}=f_\theta(x_t)$本身就是神经网络,而神经网络的权重、输入数据一般是实数域$\mathbb{R}$的,所以输出$\frac{dx}{dt} < \infty$,从而能够保证对于一个Neural ODE,存在一个$\mathrm{k_0}$使得利普希茨常数$\mathrm{Lip(NODE)}<\mathrm{k_0}$:
$$
\mathrm{Lip(NODE)} = \sup \frac{dx}{dt} = \sup_{x_t} f_\theta(x_t) < \mathrm{k_0}
$$
对于ResNet,虽然同样有神经网络输出$g_\theta(x) < \infty$,但转化为ODE形式后却无法保证$\frac{dx}{dt}$符合上述性质,因为其极限形式的分母$h\rightarrow 0$,则$\frac{1}{h} \rightarrow \infty$。虽然令$hf_\theta(x_t) = g_\theta(x_t)$可以满足,但是$f_\theta(x_t)$并不是神经网络,无法保证$f_\theta(x) < \infty$:
$$
\begin{split}
\frac{dx}{dt} & = \lim_{h\rightarrow 0} \frac{x_{t+h}-x_t}{h} \\
& = \lim_{h\rightarrow 0} \frac{g_\theta(x_t)}{h} = f_\theta(x_t)
\end{split}
$$
神经流模型的多种形式 Variants of Neural Flows
最终,普通的神经网络只需满足如下两个条件,即可认为是神经流模型。其中,对于神经网络的利普希茨连续性约束,可以用式子(15)对权重的谱范数归一化来实现:
$$
\begin{equation}
F(0, x_0) = x_0, ~~~ \mathrm{Lip}(F) < 1
\end{equation}
$$
在Neural Flows原文[8]中,提出了三种不同的流模型。首先是ResNet流模型,既然讨论了这么多可逆残差网络的内容,很自然地想到直接用上它。其中,$\phi(t)$是用来满足$F(0, x_0) = x_0$这个条件的,需要$\phi(0) = 0$。而且$\vert \phi(t) \vert < 1$,因为$\phi(t)$作为系数,会影响整体的$\mathrm{Lip}(F)$,如果$\vert \phi(t) \vert \geq 1$,整体的$\mathrm{Lip}(F)$有可能也大于$\geq 1$。$\mathrm{Lip}(g) < 1$:
$$
\begin{equation}
F(t, x) = x + \phi(t) \cdot g(t, x)
\end{equation}
$$
类似地,为了将带有循环神经网络的GRU-ODE转换为GRU流模型,作者证明了其中的系数需要满足特定取值,才能够使得模型总体的$\mathrm{Lip}(F) < 1$,证明过程较长可以阅读原文。对偶流模型主要是为了得到逆向过程的解析形式,将输入的特征维度划分为了互不相交的两组维度$A\cup B$:
$$
\begin{equation}
\begin{split}
F(t, x) & = x_A\exp\big(u(t, x_B)\phi_u(t)\big) \\
& + v(t, x_B)\phi_v(t) \\
\end{split}
\end{equation}
$$
可以看到,实际上是用B组的维度,分别送入由神经网络$u$和$v$组成的式子(17)中的ResNet流模型,作为A组特征的动态权重和偏置,同时这个结构本身是可逆的[14]。回顾之前Neural CDE笔记中的CDE动态权重推导结果,基本上保持一致。当然,这是积分层面的动态权重,而不是微分方程层面的。
最终,Neural Flows作为Neural ODE的替代品,用式子(16)中2个极其简单的约束,只需关注起点$x_0$和时间$\mathrm{T}$(注意可以随意指定时间,同样能够输出中间结果),无需复杂的数值求解器,即可达到与Neural ODE相同的性质。而这背后,是前述庞大的数学理论体系(利普希茨连续性、巴拿赫不动点定理、谱范数)作为坚实的支撑,同时也打开了一扇解读黑盒模型的全新大门,值得进一步地深入学习和应用。
参考资料
- [1] Lorenz E N. Deterministic nonperiodic flow[J]. Journal of atmospheric sciences, 1963, 20(2): 130-141.
- [2] Song Y, Ermon S. Generative modeling by estimating gradients of the data distribution[J]. Advances in neural information processing systems, 2019, 32.
- [3] Ho J, Jain A, Abbeel P. Denoising diffusion probabilistic models[J]. Advances in neural information processing systems, 2020, 33: 6840-6851.
- [4] Zhang Q, Chen Y. Diffusion normalizing flow[J]. Advances in Neural Information Processing Systems, 2021, 34: 16280-16291.
- [5] Song Y, Sohl-Dickstein J, Kingma D P, et al. Score-based generative modeling through stochastic differential equations[J]. 9th International Conference on Learning Representations, ICLR 2021.
- [6] Song J, Meng C, Ermon S. Denoising Diffusion Implicit Models [J]. 9th International Conference on Learning Representations, ICLR 2021.
- [7] Chen R T Q, Rubanova Y, Bettencourt J, et al. Neural ordinary differential equations[J]. Advances in neural information processing systems, 2018, 31.
- [8] Biloš M, Sommer J, Rangapuram S S, et al. Neural flows: Efficient alternative to neural ODEs[J]. Advances in neural information processing systems, 2021, 34: 21325-21337.
- [9] Behrmann J, Grathwohl W, Chen R T Q, et al. Invertible residual networks[C]//International conference on machine learning. PMLR, 2019: 573-582.
- [10] Ardizzone L, Kruse J, Wirkert S, et al. Analyzing inverse problems with invertible neural networks[J]. 7th International Conference on Learning Representations, ICLR 2019.
- [11] 苏剑林. 细水长flow之可逆ResNet:极致的暴力美学. https://kexue.fm/archives/6482
- [12] ReadPaper论文阅读 (IDEA研究院). Lipschitz连续及其常量的定义讲解【深度学习中的数学ep5】. https://www.bilibili.com/video/BV1B64y157DC
- [13] 苏剑林. 深度学习中的Lipschitz约束:泛化与生成模型. https://kexue.fm/archives/6051
- [14] Dinh L, Sohl-Dickstein J, Bengio S. Density estimation using real nvp[J]. 5th International Conference on Learning Representations, ICLR 2017.